www.batmath.it

Integrali doppi e tripli - Esercizi 1

1. Calcolare il volume del solido: E = {(x,y,z) | x² + y² ≤ 1, x² + z² ≤ 1}.
2. Calcolare il volume del solido: E = {(x,y,z) | (x+1)² + y² ≤ z ≤ 2x + 5}.
3. Calcolare l'integrale 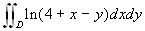, essendo D il parallelogramma di vertici (0,0), (3,3), (5,2), (2,-1).
4. Calcolare 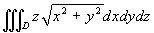, ove D = {(x,y,z) | 2z ≤ x² + y² + z² ≤ 1}.
5. Calcolare 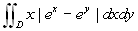, ove D = {(x,y) | 0 ≤ x ≤ 1, x² ≤ y ≤ 1}.
6. Calcolare 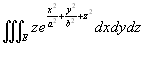, ove E è il volume compreso tra 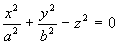e i piani z = 1 e z = 2 (a e b sono numeri positivi).
7. Calcolare 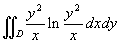, ove D è il dominio piano limitato da y² = x, y² = 2x, xy = 1, xy = 2, usando il cambiamento di variabili .
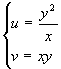8. Eseguendo un opportuno cambiamento di variabile, calcolare 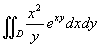, dove D è il sottoinsieme di R^2.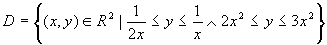

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 22/04/2004 - ultimo aggiornamento il 03/05/2004