Integrali doppi e tripli - Soluzione 1.1
Calcolare il volume del solido: E = {(x,y,z) | x2 + y2 ≤ 1, x2 + z2 ≤ 1}.
Si tratta della regione comune a due cilindri circolari retti, uno con asse coincidente con l'asse z, l'altro con asse coincidente con l'asse y.
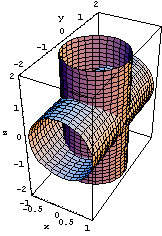
Per calcolare il volume richiesto si possono scegliere diverse strategie: integrazione per sezioni perpendicolari all'asse x, integrazione per sezioni perpendicolari all'asse z (o y), integrazione per corde. Esamineremo le diverse strategie, con lo scopo di mostrare come la scelta di una al posto di un'altra possa semplificare notevolmente i calcoli.
Integrazione per sezioni perpendicolari all'asse x
Fissato x=c, tra -1 ed 1, la sezione della regione in questione con il piano x=c si può facilmente visualizzare se si tiene conto che è la parte comune all'intersezione di detto piano con i due cilindri, cioè la regione comune a due strisce, di uguale altezza, tra di loro perpendicolari: si tratta dunque di un quadrato, la cui area è facilmente calcolabile.
.
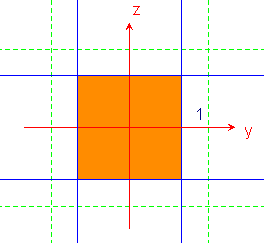
Dall'equazione di uno dei due cilindri possiamo ricavare che
, da cui si deduce che il lato del quadrato
è 
e la sua area
4(1-x2). La formula di riduzione per sezioni
(Sx è la sezione in questione)
dà dunque: .
.
Integrazione per sezioni perpendicolari all'asse y .
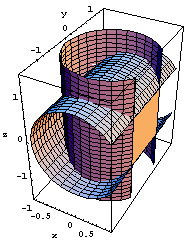
Fissiamo ora y=c, tra -1 ed 1; la sezione della regione in questione con il piano y=c si può facilmente visualizzare se si tiene conto, come prima che è la parte comune all'intersezione di detto piano con i due cilindri, cioè la regione comune a un cerchio perpendicolare all'asse y e a una striscia verticale del piano y=c. La figura che si ottiene è rappresentata, in proiezione e in due diverse visioni tridimensionali, nelle figure qui sotto.
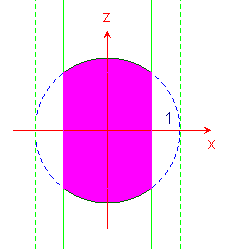
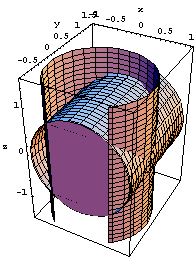
Detta Sy la sezione in questione, essa
è un dominio normale rispetto all'asse x,
nel piano xz, con la x e la z
soddisfacenti ai limiti seguenti: 
,
dove y è fissato (= c). La formula di
riduzione per sezioni dà, allora: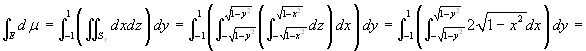 
. Per l'ultimo calcolo
abbiamo integrato per parti: 
. Come si vede
subito, con questa scelta della sezione i calcoli sono
decisamente più complessi!
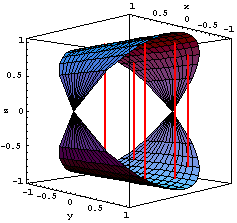
Integrazione per corde parallele all'asse z
In questo caso si tratta di fissare un punto, A, sulla proiezione della nostra regione nel piano xy e sezionare la regione stessa con una retta ("filo"), parallela all'asse z e passante per A.
Nella figura qui sotto è rappresentata la regione
interessata, vuota per poterci guardare dentro, e con alcuni
fili paralleli all'asse z. E' chiaro che la
proiezione, S, della nostra regione sul piano
xy, cioè la regione in cui varia A,
è il cerchio di centro l'origine e raggio 1. Fissato
il punto A, gli estremi di variabilità della
coordinata z sul filo sono: 
. La formula di riduzione per corde dà
allora: 
. Questa scelta della tecnica di
riduzione non comporta sostanziali difficoltà tecniche.
