Integrali doppi e tripli
Considerata una funzione f: Rn → R, e un sottoinsieme A di Rn, indicheremo l'integrale di Riemann su A (nell'ipotesi che esista!) con una delle scritture seguenti:
![]() .
.
Saremo quasi esclusivamente interessati ai casi n=2 o n=3, nel qual caso parleremo di integrali doppi o tripli. A volte, anche in presenza di indicazione esplicita delle variabili, utilizzeremo un solo segno di integrale: ∫A f(x,y,z)dxdydz. Quando poi l'insieme di integrazione sarà chiaro dal contesto, potremo anche tralasciarlo nel simbolo.
Le principali tecniche di calcolo di integrali di questo tipo si basano su una riduzione a due o tre integrazioni successive in una variabile e sul metodo del cambiamento di coordinate.
Caso di due variabili
Un sottoinsieme E di R2, del tipo E = {(x,y) | a ≤ x ≤ b, l(x) ≤ y ≤ u(x)}, con l e u funzioni continue su [a,b], è detto un dominio normale rispetto all'asse x. Analoga definizione per il dominio normale rispetto all'asse y.
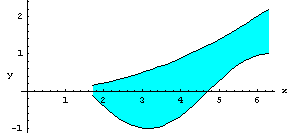
In sostanza si tratta di una regione piana in cui una delle due variabili è compresa tra due numeri a e b, mentre l'altra è compresa tra due funzioni continue della variabile precedente, definite in [a,b] e situate una più in alto e una più in basso.
![]() Sia f : E→R, una funzione continua, con E dominio normale rispetto all'asse x. Allora f è
integrabile in E e vale la seguente formula di riduzione:
Sia f : E→R, una funzione continua, con E dominio normale rispetto all'asse x. Allora f è
integrabile in E e vale la seguente formula di riduzione: 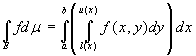 . Analoga formula di riduzione vale per le funzioni definite su domini
normali rispetto all'asse y:
. Analoga formula di riduzione vale per le funzioni definite su domini
normali rispetto all'asse y: 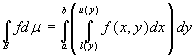 . Se l ed u sono due funzioni costanti, allora il teorema è valido in ipotesi meno restrittive della
continuità per la funzione f e si chiama teorema di Fubini: in questo caso è, di norma, possibile scambiare l'ordine di integrazione. Queste formule permettono di ridurre un integrale doppio a due integrali semplici
successivi.
. Se l ed u sono due funzioni costanti, allora il teorema è valido in ipotesi meno restrittive della
continuità per la funzione f e si chiama teorema di Fubini: in questo caso è, di norma, possibile scambiare l'ordine di integrazione. Queste formule permettono di ridurre un integrale doppio a due integrali semplici
successivi.
![]() Siano f una funzione continua sulla chiusura Ā di un aperto A misurabile di R2 e g una funzione di
Ē in Ā, dove anche Ē è la chiusura di un aperto misurabile di R2. Allora, se g è continua con le sue derivate parziali (di classe C1), biiettiva
almeno tra E ed A, e con determinante della matrice jacobiana, det(J), non nullo su E, vale la seguente formula per il cambiamento di variabile di integrazione:
Siano f una funzione continua sulla chiusura Ā di un aperto A misurabile di R2 e g una funzione di
Ē in Ā, dove anche Ē è la chiusura di un aperto misurabile di R2. Allora, se g è continua con le sue derivate parziali (di classe C1), biiettiva
almeno tra E ed A, e con determinante della matrice jacobiana, det(J), non nullo su E, vale la seguente formula per il cambiamento di variabile di integrazione: ![]() .
.
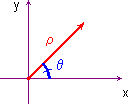
![]() Come caso di particolare importanza si ha il passaggio a coordinate polari, dove
la funzione g è data da
Come caso di particolare importanza si ha il passaggio a coordinate polari, dove
la funzione g è data da ![]() , con ρ
, con ρ ![]() [0,+∞[, θ
[0,+∞[, θ ![]() [-π,π] e determinante jacobiano uguale a ρ. Se g è sostituita da
[-π,π] e determinante jacobiano uguale a ρ. Se g è sostituita da ![]() ,
con a e b strettamente positivi, allora si parla di coordinate ellittiche e lo jacobiano vale abρ. La convenzione sui limiti per θ può anche essere, senza che nulla cambi, θ
,
con a e b strettamente positivi, allora si parla di coordinate ellittiche e lo jacobiano vale abρ. La convenzione sui limiti per θ può anche essere, senza che nulla cambi, θ
![]() [0,2π]
[0,2π]
Caso di tre variabili
Un sottoinsieme E di R3, del tipo E = {(x,y,z) | (x,y) ![]() I, l(x,y) ≤ z ≤ u(x,y)}, con l e
u funzioni continue su I, insieme chiuso e misurabile di R2, è detto un dominio normale rispetto al piano xy. Analoga definizione per il dominio normale rispetto al piano yz, o rispetto
al piano xz.
I, l(x,y) ≤ z ≤ u(x,y)}, con l e
u funzioni continue su I, insieme chiuso e misurabile di R2, è detto un dominio normale rispetto al piano xy. Analoga definizione per il dominio normale rispetto al piano yz, o rispetto
al piano xz.
![]() Sia f : E→R, una funzione continua, con E
dominio normale rispetto al piano xy. Allora f è integrabile in E e vale la seguente formula di riduzione per corde o fili paralleli all'asse z:
Sia f : E→R, una funzione continua, con E
dominio normale rispetto al piano xy. Allora f è integrabile in E e vale la seguente formula di riduzione per corde o fili paralleli all'asse z: 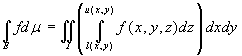 . Analoghi teoremi si ottengono scambiando i ruoli delle variabili.
. Analoghi teoremi si ottengono scambiando i ruoli delle variabili.
Questa formula permette di ricondurre l'integrale triplo ad un integrale in una variabile, seguito da un integrale doppio.
Il significato geometrico di questa riduzione appare chiaro dal grafico disegnato qui sotto, nel quale il dominio della funzione in questione è tutta la regione compresa tra la funzione "superiore", cioè u(x,y), e la funzione "inferiore", cioè l(x,y)".
Abbiamo anche rappresentato il dominio I, rispetto a cui si deve fare il secondo degli integrali che compaiono nella formula di riduzione. Si noti che il dominio I si può ritenere la proiezione del dominio normale E sul piano xy.
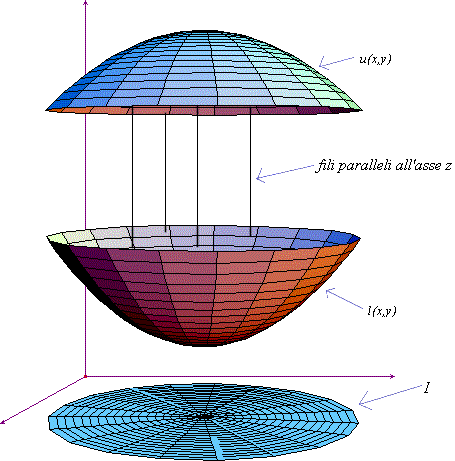
Questa formula di riduzione è sostanzialmente l'estensione a tre variabili della formula di riduzione per gli integrali doppi, che abbiamo scritto sopra.
![]() Sia f : E→R, una funzione continua, con E insieme chiuso, limitato e misurabile di R3. Indichiamo inoltre
con a e b, rispettivamente, il minimo e il massimo valore della variabile z, per i punti di E. Supponiamo inoltre che la sezione, S, di E con un piano perpendicolare all'asse z sia
misurabile (se non è vuota). Allora f è integrabile in E e vale la seguente formula di riduzione per sezioni perpendicolari all'asse z:
Sia f : E→R, una funzione continua, con E insieme chiuso, limitato e misurabile di R3. Indichiamo inoltre
con a e b, rispettivamente, il minimo e il massimo valore della variabile z, per i punti di E. Supponiamo inoltre che la sezione, S, di E con un piano perpendicolare all'asse z sia
misurabile (se non è vuota). Allora f è integrabile in E e vale la seguente formula di riduzione per sezioni perpendicolari all'asse z: 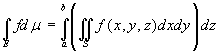 .
.
Nella figura qui sotto è rappresentato un possibile dominio del tipo considerato e tre diverse sezioni con piani perpendicolari all'asse z. In questo esempio la coordinata z varia tra -2 e 2 (si tratta degli estremi dell'ultimo integrale della formula di riduzione).
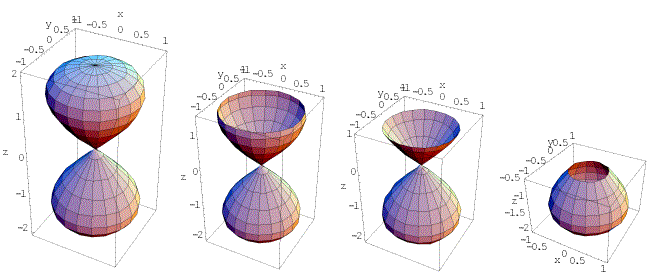
E' chiaro come si modificano le cose se si considerano sezioni perpendicolari all'asse x oppure y. La difficoltà nell'applicazione di questa formula è proprio legata alla individuazione del tipo di sezione che si ottiene a seconda del piano scelto.
![]() Siano f una funzione continua sulla chiusura Ā di un aperto A misurabile di R3 e g una funzione di
Ē in Ā, dove anche Ē è la chiusura di un aperto misurabile di R3. Allora, se g è continua con le sue derivate parziali (di classe C1), biiettiva
almeno tra E ed A, e con determinante della matrice jacobiana, det(J), non nullo su E, vale la seguente formula per il cambiamento di variabile di integrazione:
Siano f una funzione continua sulla chiusura Ā di un aperto A misurabile di R3 e g una funzione di
Ē in Ā, dove anche Ē è la chiusura di un aperto misurabile di R3. Allora, se g è continua con le sue derivate parziali (di classe C1), biiettiva
almeno tra E ed A, e con determinante della matrice jacobiana, det(J), non nullo su E, vale la seguente formula per il cambiamento di variabile di integrazione: ![]() .
.
![]() Come primo caso di particolare importanza si ha il passaggio a coordinate sferiche, o polari, dove la funzione g è data da
Come primo caso di particolare importanza si ha il passaggio a coordinate sferiche, o polari, dove la funzione g è data da 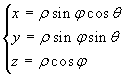 con ρ
con ρ ![]() [0,+∞[, θ
[0,+∞[, θ ![]() [-π,π] e φ
[-π,π] e φ ![]() [0,π] e
determinante jacobiano uguale a ρ2sinφ. Se g è sostituita da
[0,π] e
determinante jacobiano uguale a ρ2sinφ. Se g è sostituita da 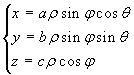 , con a, b e c strettamente positivi, allora si
parla di coordinate ellissoidali e lo jacobiano vale abcρ2sinφ. La convenzione sui limiti per θ può anche essere, senza che nulla cambi, θ
, con a, b e c strettamente positivi, allora si
parla di coordinate ellissoidali e lo jacobiano vale abcρ2sinφ. La convenzione sui limiti per θ può anche essere, senza che nulla cambi, θ ![]() [0,2π].
[0,2π].
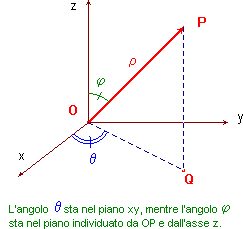
![]() Come secondo caso di particolare importanza si ha il passaggio a coordinate cilindriche, dove la funzione g è data da
Come secondo caso di particolare importanza si ha il passaggio a coordinate cilindriche, dove la funzione g è data da 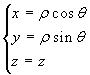 , con ρ
, con ρ ![]() [0,+∞[, θ
[0,+∞[, θ ![]() [-π,π] e nessuna limitazione per z. Lo jacobiano della trasformazione è semplicemente ρ.
[-π,π] e nessuna limitazione per z. Lo jacobiano della trasformazione è semplicemente ρ.
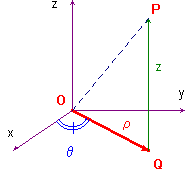
Si presti attenzione a non confondere il significato di ρ in questo sistema (dove rappresenta la distanza del punto P dall'asse z), con quello nel sistema di coordinate sferiche (dove rappresenta la distanza del punto P dall'origine).
Integrali impropri
Ricordiamo solo che per calcolare l'integrale improprio di una funzione che sia illimitata in prossimità di qualche punto di un insieme di integrazione D, oppure per calcolare l'integrale su un insieme illimitato si deve preventivamente verificare l'integrabilità della funzione e, successivamente, scegliere una qualunque successione invadente il dominio di integrazione. Solo per le funzioni di segno costante il risultato è comunque indipendente dalla scelta della successione invadente. Nella maggior parte delle applicazioni ci si trova in questo caso.