Integrali doppi e tripli - Soluzione 1.4
Calcolare 
, ove D = {(x,y,z) |
2z ≤ x2 + y2
+ z2 ≤ 1}.
Cominciamo con il valutare l'insieme D. Intanto si deve avere x2 + y2 + z2 ≤ 1, cioè si devono considerare i punti interni alla sfera di centro l'origine e raggio1. Poi 2z ≤ x2 + y2 + z2, ovvero x2 + y2 + z2 - 2z + 1 ≥ 1, x2 + y2 + (z-1)2 ≥ 1, cioè i punti esterni alla sfera di centro (0,0,1) e raggio 1.
Si può pensare questa regione come un volume di rivoluzione attorno all'asse z, nel piano tz, della regione colorata in giallo e qui sotto rappresentata.
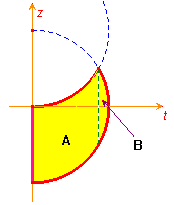
Poiché a noi interessa vedere la regione D come un dominio normale rispetto a qualche piano coordinato, possiamo immaginarla suddivisa nelle due regioni che si ottengono ruotando le superfici A e B qui sopra indicate.
La regione D e le regioni che si ottengono ruotando A e B, che possiamo chiamare D1 e D2, si possono vedere qui sotto. La seconda è raffigurata vuota per una migliore comprensione.
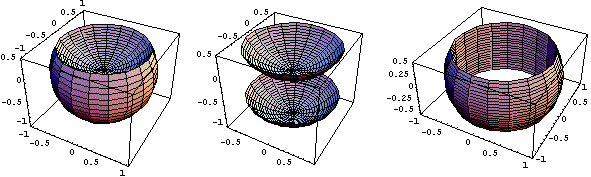
Ci interessano le proiezioni delle due regioni
D1 e D2 sul piano
xy. Anche ragionando sulla figura bidimensionale sopra
rappresentata,si vede subito che la proiezione di
D1 è la circonferenza, C,
di centro l'origine e raggio √(3)/2,
mentre la seconda è la corona circolare compresa tra
questa circonferenza e quella di centro l'origine e raggio
1. L'integrale esteso a D2 si vede
facilmente che è nullo perché il dominio
D2 è simmetrico rispetto al piano
xy, mentre la funzione integranda è dispari
rispetto a z. Per quanto riguarda l'integrale su
D1 si tratta ora di fare una riduzione per
corde. Si ottiene 
. L'integrale
residuo è abbastanza semplice da calcolare mediante una
riduzione in coordinate polari. Si ottiene il seguente
risultato: 
.