Funzioni continue
Ci occupiamo ora di un "raffinamento", in un certo senso, della nozione di limite. Precisamente ci poniamo la seguente domanda: dato un punto c del dominio di una funzione e considerato il corrispondente valore f(c), i punti "vicini" a c hanno immagine "vicina" a f(c)? La risposta è negativa, come si può vedere da alcuni degli esempi di funzione che abbiamo proposto (per esempio la funzione f(x)=|signum(x)|,dove i punti vicini a zero hanno una immagine vicina ad uno, mentre si ha f(0)=0). In sostanza l'esistenza del limite garantisce che all'avvicinarsi di x ad una dato valore c, la y si avvicina ad un certo valore l, che non ha nulla a che fare con l'eventuale valore assunto dalla funzione nel punto c (dove la funzione potrebbe benissimo non essere definita). Ora invece ci preoccupiamo di controllare se, all'avvicinarsi di x a c, la y si avvicina esattamente ad f(c).
Si dà la seguente definizione:
Una funzione 
si dice continua in un
punto c del suo dominio se, 
, ovvero, in maniera equivalente, se, 
è un intorno di c.
Si osservi che, in base alle definizioni di punto isolato e di limite, si ha:
Se il
punto c è isolato la funzione è
automaticamente continua in c, se invece il punto
c è di accumulazione la definizione precedente
equivale a dire che 
.
Si noti come, a differenza di quanto succede nella definizione di limite, qui il punto c deve essere un punto del dominio della funzione: altrimenti non avrebbe senso calcolare f(c).
Esempi:
-
La funzione
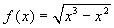è continua in
0, perché 0 è un punto isolato del dominio, che
è costituito da 0 e dai reali maggiori od uguali a 1.
-
La funzione
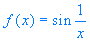non può essere continua in 0,
perché ivi non ha limite.
- La funzione f(x) = |signum(x)|, non è continua in 0, perché il limite in 0 vale 1, mentre la funzione in 0 vale 0.
-
La funzione
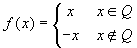, è continua
solo per x=0.
-
La funzione
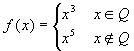, è continua per
x=0, x=1, x=-1.
Rovesciando un po' il modo di procedere da noi adottato si può osservare che il limite di una funzione in un punto c può essere considerato come la soluzione del seguente problema:
Data
una funzione e considerato un punto
c (
R) di accumulazione per D, ma
non appartenente a D, il limite della funzione per x
tendente a c, se esiste, è l'unico valore
che si può attribuire a f in c, in modo
da ottenere una funzione definita anche in c e continua
in c.
Una funzione non continua in un punto c del suo dominio si dice anche discontinua, o singolare, in c. Il concetto di singolarità è però di solito utilizzato con significato più generale come si vedrà .
Il concetto di funzione continua è di grande importanza nel calcolo dei limiti. Se infatti si riesce a concludere che una funzione è continua in un punto c del suo dominio, allora il calcolo del limite, in c, è banale: questo è esattamente quello che succede in molte delle situazioni più frequenti nelle applicazioni.
Funzioni continue su intervalli
Hanno molto interesse nelle applicazioni le funzioni continue su intervalli. Per esse valgono i seguenti teoremi, di importanza fondamentale:
Teorema di Weiertsrass: Se una funzione è continua in un intervallo chiuso e limitato essa ammette ivi sia il massimo che il minimo assoluto.
Teorema degli zeri: Se una funzione è continua in un intervallo chiuso e limitato e assume valori di segno opposto agli estremi, allora esiste almeno un punto c interno all'intervallo dove la funzione si annulla.
Il teorema di Weierstrass vale anche se l'insieme non è un intervallo, purché sia chiuso e limitato (compatto), ma questi concetti esulano dallo scopo di questa monografia.
Per quanto riguarda le funzioni continue su intervalli, spesso
si usa dire che la continuità è esprimibile
geometricamente con la condizione che la curva grafico della
funzione si può tracciare "senza staccare la
penna dal foglio". La nozione, seppur
significativa in casi elementari, non ha alcuna giustificazione,
come mostra la funzione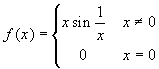 
che è
ovunque continua, ma che non può essere tracciata in
quanto la sua lunghezza è infinita, anche se ci si limita
ad una piccolo intervallo circondante lo zero. La cosa diventa
ancora più drammatica se si considerano funzioni come la
scala diabolica, o altre che
intervengono nello studio dei frattali.
Algebra delle funzioni continue
É una conseguenza immediata dei teoremi sull'algebra dei limiti che la somma, il prodotto, il quoziente di due funzioni continue è ancora una funzione continua.
Si tenga però presente che, come osservato anche a proposito dell'analogo problema sui limiti, la somma (il prodotto, il quoziente) di due funzioni non continue può benissimo essere continua. Si vedano gli esempi che seguono:
-
Le funzioni
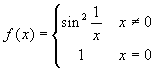e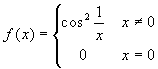 
non sono continue (in zero), mentre la loro
somma vale costantemente 1, per cui è sicuramente
continua.
-
La funzione
non è continua
(in zero), ma il suo prodotto con la funzione f(x)=x
(ovunque continua), è ovunque continua.
-
La funzione
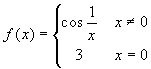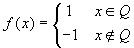non è continua
in nessun punto, ma la funzione 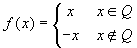, ottenuta mediante prodotto con la funzione
f(x)=x è continua almeno in zero.
-
Un esempio che mostra quanto strana possa essere una funzione
continua, rispetto all'idea intuitiva di funzione che si
può tracciare "senza staccare la penna dal
foglio":
. La funzione, come si
può provare,
è continua su tutti i punti irrazionali e discontinua
su tutti i punti razionali.
Continuità della funzione composta
Siano date due funzioni f e g, tali che si
possa considerare la composta 
. Vale il seguente fondamentale teorema:
Se f è una funzione continua in un punto
c e g è continua nel punto
f(c), allora la funzione composta è continua in c.
La dimostrazione è una conseguenza quasi immediata della definizione.
Poniamo a=f(c) e b=g(a)=g(f(c)). Preso
un intorno U di b, V=g
-1(U) è un intorno di a
per la continuità di g, mentreT
=f-1(V)=f-1(g -1(U))
è un intorno di c per la continuità
di f. Se teniamo conto che 
, si conclude subito.
Si noti che anche questo teorema esprime solo una condizione sufficiente: la composta di due funzioni non continue può benissimo essere continua. Basta prendere, ad esempio, per f una funzione qualunque e per g una funzione costante: la composta sarà costante e dunque continua
Funzioni inverse e continuità
Una funzione è invertibile se (e solo se) è biunivoca. La continuità impone delle condizioni molto restrittive alle funzioni invertibili. In particolare:
Se una funzione è definita su un intervallo ed è ivi continua, allora essa è invertibile se e solo se è crescente [decrescente]. Inoltre la funzione inversa è anch'essa continua e crescente [decrescente].
Osservazioni:
-
Una funzione non continua, anche se definita su un
intervallo, può benissimo essere invertibile senza
essere crescente [decrescente]: un esempio è
fornito da .
-
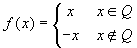Una funzione continua, non definita su un intervallo, e
invertibile, può benissimo avere inversa non continua.
I grafici qui sotto rappresentano una funzione f
(quello a sinistra) definita in [a,b]
]c,d]
e continua. La sua inversa (grafico a destra) è
palesemente discontinua nel punto e.
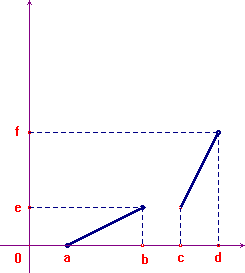
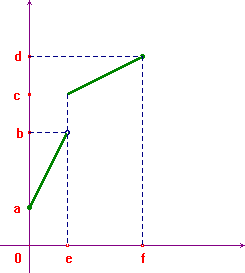
- Una funzione, anche non continua, se è definita in un intervallo ed è crescente [decrescente], ha sempre inversa continua. Un esempio si ottiene dai due grafici qui sopra, interpretando quello di destra come la funzione f e quello di sinistra come la sua inversa.