Definizione di limite
Un primo approccio
Il problema di cui ci vogliamo occupare è, con linguaggio
intuitivo, il seguente: consideriamo una funzione definita in un
insieme D (dominio) e avente c (anche
infinito) come punto di accumulazione. Sia poi x un
punto qualunque, appartenente a D, e calcoliamo il
corrispondente valore f(x). Immaginiamo ora di muovere
x, facendolo avvicinare "quanto si vuole" a
c, ma sempre rimanendo in D: che cosa
succederà dei corrispondenti valori di f(x)? Se
succede che f(x) si avvicina ad un determinato valore
(anche infinito), diciamolo l, allora diremo che
l è il limite, per x tendente a
c, di f(x) e scriveremo ![]() o anche
o anche ![]() .
.
Per capire il problema consideriamo come esempio la funzione
![]() e il punto c=0.
e il punto c=0.
Nella tabella qui di seguito abbiamo riportato nella prima
colonna i valori di x (sempre più
"prossimi" a zero) e i corrispondenti valori di ![]() che, come si può facilmente vedere,
sono sempre più "prossimi" ad uno. Con la
"definizione" data sopra potremo dire che
che, come si può facilmente vedere,
sono sempre più "prossimi" ad uno. Con la
"definizione" data sopra potremo dire che ![]() .
.
| x |
|
| 1 | 0.8414709848 |
| 0.5 | 0.9588510772 |
| 0.3 | 0.9850673555 |
| 0.2 | 0.9933466540 |
| 0.1 | 0.9983341665 |
| 0.05 | 0.9995933854 |
| 0.01 | 0.9999833334 |
| 0.005 | 0.9999958333 |
| 0.0001 | 0.9999998333 |
É chiaro che una "definizione" di questo tipo non è per nulla accettabile dal punto di vista matematico: infatti anche se dalla tabella sembra chiaro che i valori di f(x) si approssimano ad uno, nulla ci garantisce che il comportamento rimanga "stabile" "comunque vicino ci mettiamo a zero".
Purtroppo una definizione rigorosa non è facile e soprattutto non è possibile tradurre in una precisa formulazione il concetto "dinamico" implicito nel modo di procedere che risulta dall'esempio sopra citato. Storicamente c'è voluto parecchio tempo prima che si riuscisse a trovare una formulazione corretta ed esente da critiche. Un passo avanti sensibile lo fece Cauchy, ma è solamente con Karl Weierstrass che si arriva al concetto nella forma ancora oggi ritenuta valida. La prima pubblicazione ufficiale avviene comunque ad opera di H.E.Heine, un allievo dello stesso Weierstrass, in Elemente, nel 1872.
La definizione rigorosa
Nella definizione di limite si ragiona nel seguente modo:
dato un punto c (anche infinito) di
accumulazione per il dominio di una funzione (il fatto che
c sia di accumulazione ci garantisce che è
possibile calcolare f(x) in infiniti punti nei pressi
di c) e dato un certo numero l (che per ora
non ci preoccupiamo di sapere come è stato determinato),
ci piazziamo nei pressi di l, secondo un ordine di
vicinanza arbitrario, cioè consideriamo un intorno
arbitrario di l, e analizziamo quali sono i punti
immagine di f che cadono in questo intorno arbitrario,
cioè consideriamo tutte le frecce che sono
cadute in questo intorno arbitrario. Se, tra gli arcieri che
hanno sparato queste frecce, ci sono anche tutti quelli
che stanno in un opportuno intorno di c,
escluso al più c stesso di cui non vogliamo
occuparci, allora possiamo affermare che ![]() , altrimenti no. Si noti che non abbiamo
affatto escluso che di arcieri che hanno sparato queste frecce
ce ne siano anche altri "lontani" da c,
quello che conta è che ci siano tutti quelli che
stanno in almeno un opportuno intorno di c
escluso al più c stesso. L'idea che
sta alla base della definizione è che, in un certo senso,
bisogna "cambiare ottica": invece di mettersi a
guardare le cose dal punto di vista delle "x che si
avvicinano a c", come parrebbe naturale, occorre
piazzarsi sul codominio, in un intorno del punto l, e
controllare quali sono le x che hanno immagine
appartenente a questo intorno di l. Sparisce
così l'idea di "movimento di x verso
c".
, altrimenti no. Si noti che non abbiamo
affatto escluso che di arcieri che hanno sparato queste frecce
ce ne siano anche altri "lontani" da c,
quello che conta è che ci siano tutti quelli che
stanno in almeno un opportuno intorno di c
escluso al più c stesso. L'idea che
sta alla base della definizione è che, in un certo senso,
bisogna "cambiare ottica": invece di mettersi a
guardare le cose dal punto di vista delle "x che si
avvicinano a c", come parrebbe naturale, occorre
piazzarsi sul codominio, in un intorno del punto l, e
controllare quali sono le x che hanno immagine
appartenente a questo intorno di l. Sparisce
così l'idea di "movimento di x verso
c".
Sia data una funzione f definita in un certo insieme
D e sia c (anche infinito) un punto di
accumulazione per D. Si dice che ![]() (l può anche essere
infinito) se,
(l può anche essere
infinito) se, ![]() .
.
Si noti come in questa definizione non ci sia alcuna indicazione su come si possa ricavare l: ci si preoccupa solo di controllare se un dato l verifica o no una certa condizione relativa a tutti i suoi intorni. Il problema di come calcolare questo valore l è estremamente complesso e sarà affrontato in seguito.
La definizione appena data ha una semplice interpretazione grafica. Si consideri un intorno Ul (un segmento o una semiretta); a partire da esso si stabilisca se esiste oppure no un intorno Uc in modo tale che il grafico della funzione ristretta ai punti di Uc stia completamente entro la striscia orizzontale individuata da Ul.Se il problema (che ha dunque come "incognita" l'intorno Uc) ha una soluzione allora il limite è l, altrimenti no.
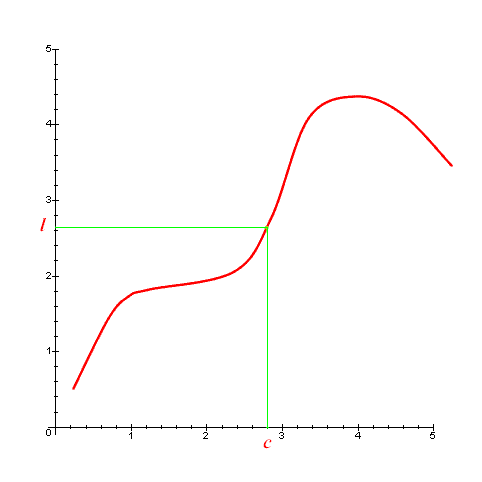
Nelle figure che proponiamo di seguito si considera una funzione f(x) e il suo grafico, un punto c sull'asse delle ascisse e un punto l sull'asse delle ordinate.
Considerati alcuni intorni di l, si verifica che
è sempre possibile trovare un intorno di c in
modo che il grafico della funzione, ristretta a questo intorno
di c, cada nella striscia verticale delimitata
dall'intorno di l: si può dunque affermare
che ![]() . Si noti,
nella sequenza di immagini, che l'intorno di c si
può sempre trovare anche se l'intorno di l
diventa "infinitamente piccolo". É
evidente, d'altra parte, che il problema della ricerca
dell'intorno di c ha tanto minori
probabilità di soluzione quanto più l'intorno
di l è piccolo (se per esempio l'intorno di
l fosse tutta la retta non occorrerebbe fare alcuna
ricerca dell'intorno di c, ovviamente!).
. Si noti,
nella sequenza di immagini, che l'intorno di c si
può sempre trovare anche se l'intorno di l
diventa "infinitamente piccolo". É
evidente, d'altra parte, che il problema della ricerca
dell'intorno di c ha tanto minori
probabilità di soluzione quanto più l'intorno
di l è piccolo (se per esempio l'intorno di
l fosse tutta la retta non occorrerebbe fare alcuna
ricerca dell'intorno di c, ovviamente!).
- Immagine iniziale
- Primo intorno
- Secondo intorno
- Terzo intorno
- Quarto intorno
- Quinto intorno
- Sesto intorno
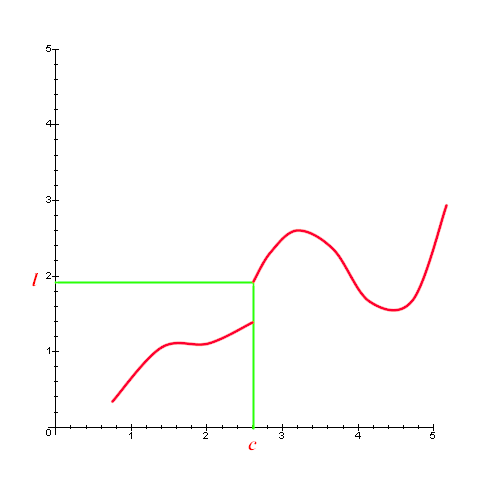
Naturalmente il limite non esiste sempre (altrimenti che gusto
ci sarebbe?). Si consideri per esempio la funzione il cui
grafico è rappresentato qui sotto, e siano c ed
l i valori indicati. Se si considera un intorno
"grande" di l si riesce a
determinare un intorno di c soddisfacente alle
condizioni richieste nella definizione di limite; se però
si considera un intorno "abbastanza piccolo"
di l la cosa non è possibile, basta osservare
che un qualunque punto a sinistra di c ha
un'immagine che non sta nell'intorno scelto: ne consegue
che l non è il limite della funzione, per x
tendente a c. Si può capire facilmente anche
come, in questo caso, non esista alcun valore di l che
sia adatto: il ![]() .
.
- Grafico iniziale
- Intorno "grande" di l
- Intorno "piccolo" di l
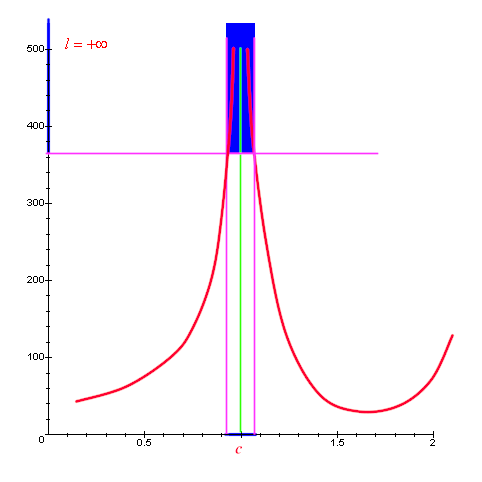
La definizione di limite che abbiamo dato è basata
unicamente sulla topologia, cioè sul concetto di intorno
(sulla retta ampliata in uno dei due modi indicati) e non
necessita di alcuna distinzione tra i casi di limiti in cui
c o l siano finiti o infiniti. Per precisare
le varie situazioni che si possono presentare riportiamo
comunque più sotto alcune rappresentazioni grafiche, ricordando che
quando si usa il simbolo "∞" si intende la retta
ampliata con un solo punto, quando si usano i simboli
"+∞"
e"-∞" si intende la retta ampliata con due
punti.
Osservazioni
![]() - Tra
tutti gli intorni di un numero reale c ci
interesseranno in maniera particolare gli intervalli che hanno
centro nel punto stesso: li chiameremo Intorni circolari e
indicheremo abitualmente con ε (epsilon) la loro
semiampiezza. L'importanza degli intorni circolari, in
particolare nella "verifica di limiti", risulta dal
fatto che, come si può provare, nella definizione di
limite ci si può limitare a considerare solo gli intorni
circolari di l, anziché esaminare tutti gli
intorni. In termini formali si può dire che gli intorni
circolari costituiscono una base di intorni, e che ,
nella definizione di limite ci si può limitare a
considerare questa base di intorni di l. Anche per gli
intorni di c sarebbe sufficiente limitarsi a questa
base di intorni, ma la cosa è, praticamente, poco utile.
Il concetto di intorno circolare si può estendere anche
al caso di ∞ : basterà considerare l'unione di
due semirette del tipo
- Tra
tutti gli intorni di un numero reale c ci
interesseranno in maniera particolare gli intervalli che hanno
centro nel punto stesso: li chiameremo Intorni circolari e
indicheremo abitualmente con ε (epsilon) la loro
semiampiezza. L'importanza degli intorni circolari, in
particolare nella "verifica di limiti", risulta dal
fatto che, come si può provare, nella definizione di
limite ci si può limitare a considerare solo gli intorni
circolari di l, anziché esaminare tutti gli
intorni. In termini formali si può dire che gli intorni
circolari costituiscono una base di intorni, e che ,
nella definizione di limite ci si può limitare a
considerare questa base di intorni di l. Anche per gli
intorni di c sarebbe sufficiente limitarsi a questa
base di intorni, ma la cosa è, praticamente, poco utile.
Il concetto di intorno circolare si può estendere anche
al caso di ∞ : basterà considerare l'unione di
due semirette del tipo ![]() , con a reale
positivo. Il teorema citato vale anche in questo caso.
, con a reale
positivo. Il teorema citato vale anche in questo caso.
![]() - In modo perfettamente analogo si può provare che, nella
definizione di limite, è sufficiente considerare solo gli
intorni piccoli quanto si vuole di l (
- In modo perfettamente analogo si può provare che, nella
definizione di limite, è sufficiente considerare solo gli
intorni piccoli quanto si vuole di l (![]() R), nel senso che, se necessario, ci si
può limitare a considerare solo gli intorni minori di un
qualsivoglia numero positivo scelto a piacere. Tenendo conto
anche dell'osservazione precedente possiamo concludere che
è lecito limitarsi a considerare solo intorni circolari
di l, con ampiezza ε minore di un qualsivoglia
numero positivo fissato a piacere. In sostanza, se osserviamo
che, con questo tipo di intorni, dire
R), nel senso che, se necessario, ci si
può limitare a considerare solo gli intorni minori di un
qualsivoglia numero positivo scelto a piacere. Tenendo conto
anche dell'osservazione precedente possiamo concludere che
è lecito limitarsi a considerare solo intorni circolari
di l, con ampiezza ε minore di un qualsivoglia
numero positivo fissato a piacere. In sostanza, se osserviamo
che, con questo tipo di intorni, dire ![]() significa dire
significa dire ![]() , possiamo concludere che,
nel caso di l
, possiamo concludere che,
nel caso di l![]() R, la definizione di limite può essere
semplificata nel seguente modo:
R, la definizione di limite può essere
semplificata nel seguente modo:
![]()
Il concetto si può estendere anche agli intorni sulla
retta estesa, basterà prendere semirette (o unioni di
semirette) ![]() , con a "grande
quanto si vuole".
, con a "grande
quanto si vuole".
![]() - Una
ulteriore proprietà , molto utile
nelle dimostrazioni dei teoremi sui limiti, è la
seguente: nel caso di l
- Una
ulteriore proprietà , molto utile
nelle dimostrazioni dei teoremi sui limiti, è la
seguente: nel caso di l![]() R, per verificare che
R, per verificare che ![]() , ci si può limitare, meno
restrittivamente, a verificare che
, ci si può limitare, meno
restrittivamente, a verificare che ![]() , con
k numero positivo assegnato a piacere.
, con
k numero positivo assegnato a piacere.