Funzione
Il concetto di funzione è uno dei più fecondi della matematica ed è opportuno avere idee chiare e precise su di esso per evitare di incorrere in errori anche madornali.
Una funzione è una legge, che si può indicare con f, che associa ad ogni punto di un insieme A detto dominio uno ed un solo punto di un insieme B detto codominio. In termini ancora più precisi una funzione è un sottoinsieme, f, del prodotto cartesiano A×B, tale che, per ogni elemento a di A esiste uno ed un solo elemento b di B, per cui \((a,b)\in f\subset A\times B\).
L'insieme A può essere pensato come un insieme di arcieri, l'insieme B come un insieme di bersagli. É molto importante il fatto che ogni arciere dispone di un'unica freccia che è costretto a lanciare, mentre non c'è alcuna limitazione sui bersagli da colpire: può benissimo succedere che tutti gli arcieri lancino le frecce sullo stesso bersaglio (nel qual caso la funzione si dice costante), o che ciascun arciere spari la propria freccia su un diverso bersaglio (nel qual caso la funzione si dice iniettiva), o che tutti i bersagli vengano colpiti almeno una volta (nel qual caso la funzione si dice suriettiva). Gli elementi di A si indicano con x, quelli di B con y e per indicare che la freccia x colpisce il bersaglio y si scrive \(y=f(x)\). L'insieme di tutti i bersagli che vengono colpiti almeno una volta si dice insieme immagine di A tramite la funzione e si può indicare con \(f(A)\). Bisogna prestare molta attenzione a non confondere il codominio con l'insieme immagine.
La scrittura più completa per le funzioni è: \[\begin{array}{c}f : A\to B\\x\mapsto f(x)\end{array}\,.\] Se poi il dominio e il codominio sono già noti o evidenti dal contesto, si scrive semplicemente \(x\mapsto f(x)\). Spesso si usa anche la scrittura ridotta \(y=f(x)\), anche se con essa possono sorgere equivoci.
Abitualmente si usano rappresentazioni grafiche come quella qui sotto riportata per visualizzare le funzioni.
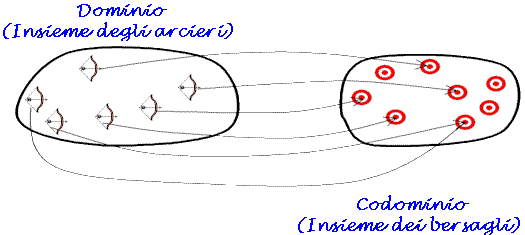
Queste rappresentazioni sono molto significative per taluni aspetti, ma possono trarre in inganno per altri, in ogni caso sono prive di qualunque interesse nel caso gli insiemi A e/o B siano infiniti (che è il caso di maggiore interesse). Nel caso particolare di funzioni che abbiano come dominio e codominio sottoinsiemi di \(\mathbb{R}\), è uso comune rappresentare sia A che B su due rette incidenti (di solito ortogonali), dette assi cartesiani. Le frecce che congiungono ciascun punto di A con il corrispondente punto di B si rappresentano allora con tratti paralleli agli assi e anzi, per evitare eccessivo affollamento di frecce nel grafico, di queste frecce si rappresenta di solito solo lo "spigolo". L'insieme di tutti questi "spigoli" è quello che comunemente si chiama "grafico" di una funzione (reale di variabile reale). L'esame di questo "grafico" può fornire utili ed interessanti elementi per scoprire le caratteristiche importanti di questo tipo di funzioni.
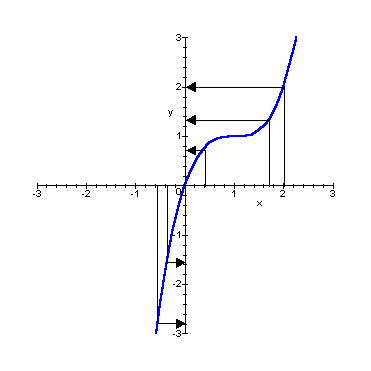
Nella figura qui sotto è riportato il "grafico" cartesiano di una funzione che ha dominio e codominio coincidenti con l'insieme di tutti i numeri reali.
Come si può dedurre dal grafico l'insieme dominio è rappresentato sull'asse orizzontale (asse delle ascisse), mentre l'insieme codominio è rappresentato sull'asse verticale (asse delle ordinate). Le frecce che collegano i punti del dominio con quelli del codominio sono infinite ed è impossibile rappresentarle tutte. Un interessante compromesso è quello di rappresentare solo gli "spigoli" di queste frecce che, tutti insieme, danno la linea rappresentata in blu. Il solo esame di questa linea fornisce indicazioni molto importanti per lo studio delle proprietà della funzione e per le applicazioni in tutti i campi. É bene comunque tenere presente che non sempre le funzioni hanno come grafico una "linea" nel senso intuitivo del termine.
Puoi vedere un'animazione con Cabri di questa costruzione.
Alcuni problemi connessi con la terminologia correntemente utilizzata per le funzioni si possono trovare nella pagina Funzioni e terminologia.