L'algebra dei limiti
Il problema che vogliamo affrontare è il seguente: se due funzioni, f e g, hanno limite, per x tendente a c, che ne è del limite della somma delle due funzioni, del prodotto, del quoziente?
Si tratta di una questione molto importante per quanto riguarda
il calcolo dei limiti. Ci interessa
anche segnalare che questo problema viene sempre affrontato
quando si introduce una nuova operazione o funzione sui reali o
sulle funzioni reali di variabile reale, come si può
vedere su alcuni esempi riportati nella tabella che segue.
|
Il reciproco di una somma non è la somma dei reciproci. |
|
La radice di una somma non è la somma delle radici |
|
Il modulo di una somma è minore od uguale alla somma dei moduli |
|
Il seno di una somma non è la somma dei seni |
|
Il logaritmo di una somma non è la somma dei logaritmi |
La questione si può formulare in termini di invertibilità nell'ordine di esecuzioni delle operazioni: dati due numeri a e b non è consentito scambiare l'ordine, per esempio, tra le operazioni di somma e di passaggio al reciproco, ovvero non si ottiene lo stesso risultato se prima si esegue la somma e poi si passa al reciproco oppure se prima si fa il reciproco e poi si esegue la somma.
Nel caso del limite la risposta al problema posto è relativamente semplice nel caso le due funzioni abbiano limite finito, come si può facilmente dimostrare, più complessa nel caso almeno uno dei due sia infinito.
Il limite del modulo di una funzione
Prima di affrontare il problema del limite di una somma, prodotto o quoziente, premettiamo la seguente osservazione:
Se, per una funzione f, si ha 
, si ha anche 
.
La dimostrazione è una conseguenza immediata della
disuguaglianza: 
. Se dunque 
, a maggior ragione 
.
Questa importante proprietà del limite del modulo di una
funzione non si può invertire. Un esempio è dato
dalla funzione 
, che non ha limite per
nessun x, mentre il suo valore assoluto vale sempre 1 e
dunque ha chiaramente limite 1 per ogni x.
Il caso dei limiti entrambi finiti e con denominatore che non tende a zero
Siano f e g due funzioni aventi c come punto di accumulazione del dominio. Si supponga inoltre che le due funzioni abbiano, per x tendente a c, limiti finiti l ed m. Allora:
-
-
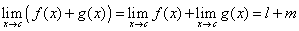visualizza la dimostrazione
Se f tende a l e g tende a m per x tendente a c, significa che, in un intorno opportuno, U, di c, si ha
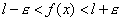, e in un altro intorno, V, si
ha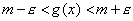 
.
Nell'intersezione dei due intorni le
disuguaglianze varranno contemporaneamente e
potranno essere sommate membro a membro, ottenendo:
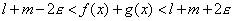. Questo basta
per concludere.
-
-
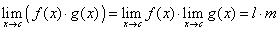visualizza la dimostrazione
Per la dimostrazione si può innanzitutto osservare che:
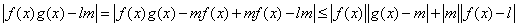. Per la proprietà del
limite del modulo di una funzione si ha: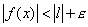 
. Se ne deduce
che: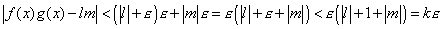 
. Per
l'ultima disuguaglianza abbiamo utilizzato il
fatto che si può supporre ε<1.
Questo basta per concludere.
-
Se inoltre m≠0, allora
-
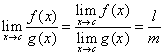visualizza la dimostrazione
Per la dimostrazione si osservi, intanto, che
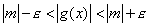(limite del
modulo di una funzione). Se si suppone ora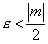 
, si trova:
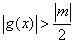. Si procede
ora con la catena di disuguaglianze e uguaglianze:
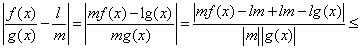
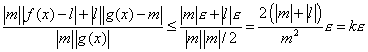. Questo basta
per concludere.
Il caso in cui almeno uno dei due limiti è infinito o il denominatore tende a zero
Siano f e g due funzioni aventi c come punto di accumulazione del dominio. Si supponga inoltre che le due funzioni abbiano, per x tendente a c, limiti l ed m, di cui almeno uno non finito. Per trattare questo caso è opportuno estendere, almeno parzialmente, la struttura algebrica presente su R alla retta reale estesa (con uno o due punti). Si possono dare le seguenti definizioni:
!!Nelle definizioni seguenti a è un numero reale qualunque, mentre A è un numero reale non nullo!!
- a ± (+∞) = ±∞;
-
a ± (-∞) =
∞;
- (+∞) + (+∞) = +∞;
- (-∞) + (-∞) = -∞;
- A×(∞) = ∞ (con la usuale regola dei segni);
- (∞)×(∞) = ∞ (con la usuale regola dei segni);
-
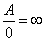(con la
usuale regola dei segni; anche zero può avere un segno
in questo contesto, come diremo subito);
-
;
-
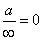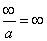(con la usuale
regola dei segni).
Ciascuna delle definizioni date costituisce l'enunciato di un teorema sull'algebra dei limiti. Per esempio a ± (+∞) = ±∞ è la scrittura abbreviata del seguente teorema:
Siano f e g due funzioni aventi c come punto di accumulazione del dominio. Si supponga inoltre che le due funzioni abbiano, per x tendente a c, limiti a e +∞, allora la somma (differenza) delle due funzioni ha limite +∞ (-∞).
La dimostrazione di questi teoremi è molto semplice e può essere fatta con la stessa tecnica usata per le dimostrazioni nel caso dei limiti finiti.
Per quanto riguarda il segno di zero, intendiamo che se il limite di una funzione in un punto c vale zero e la funzione è positiva (negativa) in un intorno di c, allora lo zero è positivo (negativo), altrimenti non ha segno.
Forme indeterminate
Si osservi che non sono state definite le seguenti operazioni:
- (+∞) - (+∞); (-∞) + (+∞); (-∞) - (-∞); (+∞) + (-∞); (∞)± (∞)
- 0×(∞)
-
-
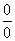
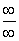
Questo significa che, nei casi indicati, non è possibile
stabilire regole generali per prevedere quale sarà il
limite di una somma, prodotto o quoziente di due funzioni. Si
considerino le funzioni: 
. Per x
tendente a zero le prime due hanno limite zero, le ultime due
hanno invece limite infinito. Considerando il prodotto di due di
esse si ha: 
, nonostante in tutti e
tre i casi si tratti del prodotto di uno "zero" per un
"infinito".
Con un linguaggio abbastanza improprio le quattro situazioni indicate sono definite forme indeterminate. Questo non significa che i limiti sono indeterminati o non calcolabili, ma solo che non esistono teoremi "algebrici" che possano risolvere immediatamente la situazione: occorre considerare separatamente ciascun caso, e non esistono tecniche standard da applicare. Sarebbe più appropriata una espressione del tipo forme difficili, in quanto ogni limite costituisce un caso a sé.
Considerando le funzioni del tipo f(x)g(x),
si possono incontrare altre situazioni di questo tipo. Tenendo
infatti conto dell'uguaglianza: 
, si trova, con scrittura largamente informale:
-
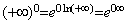: forma indeterminata.
-
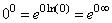: forma indeterminata.
-
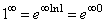: forma indeterminata.
Si noti come, invece, 
.