www.batmath.it

Fasci di circoli

Definizione

Si chiama fascio di circoli l'insieme di tutti i circoli del piano aventi a due a due lo stesso asse radicale, che si chiama asse radicale del fascio.

Il caso in cui l'asse radicale è all'infinito è speciale: in questa situazione il fascio di circoli è costituito da tutti i circoli del piano aventi lo stesso centro.

Un fascio di circoli ha una definizione simile a quella di fascio di rette: nel caso delle rette un fascio è costituito da tutte le rette che hanno in comune un punto o la direzione (la direzione può anche essere considerata uno speciale punto all'infinito); nel caso dei circoli il fascio è costituito dai circoli che hanno in comune l'asse radicale (eventualmente mandata all'infinito).

I centri dei cerchi del fascio sono allineati su una retta perpendicolare all'asse radicale, detta asse centrale del fascio, anche se non tutti i punti di quest'asse possono essere centri di circoli del fascio. Nel caso di un fascio di circoli concentrici l'asse centrale è indeterminata.

Un fascio è definito non appena sono noti due circoli del fascio o un circolo e l'asse radicale; analogamente al fascio di rette, un fascio di circoli può essere considerato, analiticamente, come l'insieme di tutte le combinazioni lineari di due dati circoli, che possono essere considerati i circoli base del fascio (oppure di un circolo e di una retta, che sarà l'asse radicale del fascio). A seconda della posizione relativa dei due circoli base (o del circolo e dell'asse radicale) si hanno diversi tipi di fascio.

Gli eventuali punti comuni  a tutti i circoli del fascio si dicono punti base. Tra tutti i circoli del fascio ve ne possono essere al massimo due che hanno raggio nullo: essi si chiamano punti limite del fascio. La denominazione di punti limite è dovuta a J.V.Poncelet, ed è per questo che questi punti sono anche noti con il nome di punti di Poncelet. Il numero complessivo dei punti base e dei punti limite non può essere maggiore di due (nel campo reale in cui noi ci siamo posti).

Tipi di fasci

• Fascio di circoli secanti
• Fascio di circoli tangenti
• Fascio di circoli a punti limite
• Fascio di circoli concentrici

Teorema generale sui fasci di circoli

In un fascio di circoli esiste uno ed un solo circolo passante per un dato punto P del piano, diverso dagli eventuali punti base. Se il punto P sta sull'asse radicale il circolo passante per P è lo stesso asse radicale che si può considerare come un circolo del fascio a raggio infinito.

La costruzione è evidente nel caso di un fascio di circoli secanti (cerchio per P e per i due punti comuni), tangenti (cerchio per P e tangente in A all'asse radicale) o concentrici. Nel caso di un fascio a punti limite, congiunto P con i punti limite L ed M, si tratta di tracciare le bisettrici dell'angolo interno ed esterno di vertice P del triangolo LPM: i suoi punti A e B di intersezione con la retta LM sono estremi di un diametro del cerchio richiesto (per la nota proprietà delle bisettrici degli angoli di un triangolo). Si veda, per questo caso, la figura qui sotto e l'animazione della stessa figura con CabriJava.

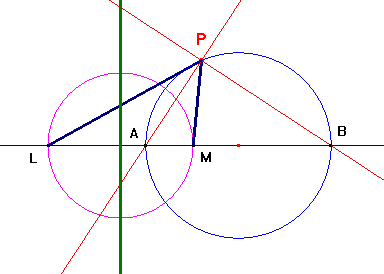
Cerchi di un fascio come luogo geometrico

Come è noto, dati due circoli qualunque non concentrici, nel piano l'asse radicale è il luogo dei punti del piano che hanno uguale potenza rispetto ai due circoli, ovvero tali che il rapporto delle potenze sia k=1. Generalizzando ci si può chiedere qual'è il luogo dei punti del piano tali che il rapporto delle potenze rispetto ai due circoli sia un reale k≠1. Come ora proveremo, questo luogo è un particolare circolo del fascio individuato dai due circoli dati.

Il luogo geometrico dei punti del piano che hanno potenze di rapporto costante k≠1, rispetto a due circoli fissati di centri C e C', è il circolo del fascio individuato dai due circoli dati e avente centro nel punto O che divide il segmento orientato CC' nel rapporto (algebrico) k.

Tralasciamo la dimostrazione, un po' complessa in termini sintetici.

Puoi vedere un'animazione con CabriJava. In particolare questa animazione mostra  che il luogo richiesto può anche essere vuoto per certi valori di k nel caso in cui i due circoli dati non abbiano punti comuni. Infatti in questo caso non tutti i punti dell'asse centrale possono essere centri di circoli del fascio, ma solo quelli non interni al segmento che congiunge i punti limite. 

La situazione in cui i due circoli base sono concentrici è speciale da questo punto di vista. Se infatti O coincide con O' il luogo richiesto è costituito dai punti Q tali che QO²-r²=k(QO²-r'²), ovvero: (1-k)QO²=r²-kr'². Si tratta cioè di un cerchio concentrico ai due cerchi base. 

Fasci ortogonali.

Dato un fascio di circoli si può considerare l'insieme di tutti i circoli ortogonali a ciascun circolo del fascio. Non è difficile provare (e invitiamo il lettore interessato a farlo per utile esercizio) che l'insieme di tutti questi circoli, tranne nel caso di un fascio di circoli concentrici, è a sua volta un fascio di circoli, che si dice coniugato del fascio dato. Questo nome deriva dal fatto che i due fasci di circoli si scambiano l'asse radicale e l'asse centrale. Valgono inoltre le seguenti proprietà:

Fascio di circoli secanti. Il fascio coniugato è un fascio a punti limite, avente come punti limite proprio i punti base del fascio dato.

Fascio di circoli a punti limite. Il fascio coniugato è un fascio di circoli secanti, avente come punti base i punti limite del fascio dato.

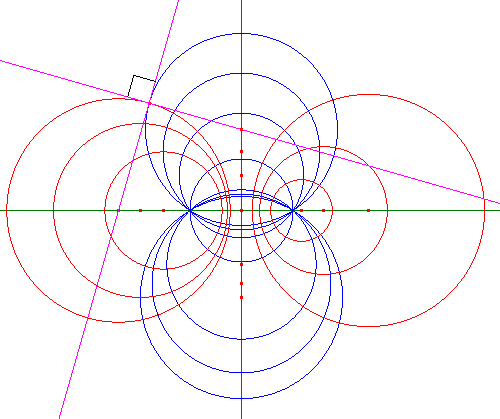
Fascio di circoli tangenti. Il fascio coniugato è ancora un fascio di circoli tangenti, con lo stesso punto di tangenza.

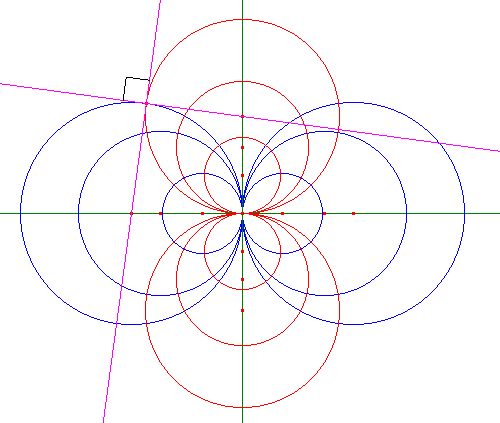
Fascio di circoli concentrici. In questo caso non esiste fascio coniugato, mentre tutti i circoli del fascio sono ortogonali alle rette del fascio che ha centro nel centro comune dei circoli.

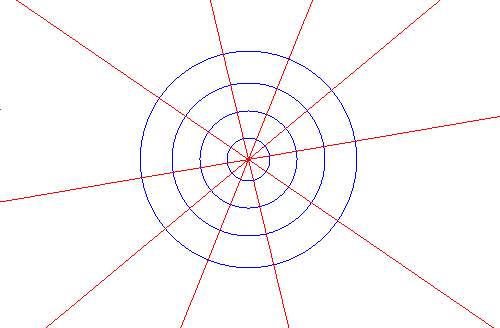
Una applicazione utile dei fasci ortogonali si ha in alcune costruzioni geometriche. Ne citiamo due.

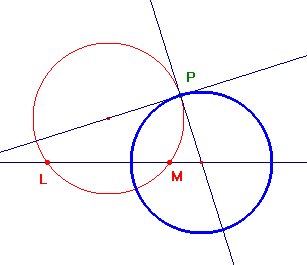
Costruire il circolo di un fascio a punti limite, passante per un dato punto P (Metodo alternativo a quello sopra riportato).

Dati i punti limite L ed M ed il punto P, si costruisce il cerchio passante per questi tre punti (in rosso nella figura). Il cerchio che cerchiamo deve essere, in P, ortogonale a questo cerchio. Se teniamo conto che deve avere centro sulla retta LM la sua costruzione è immediata.

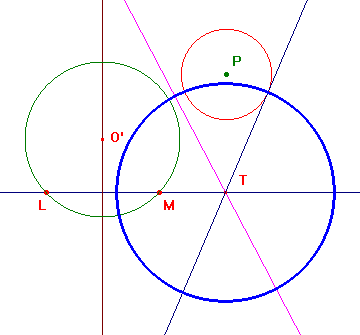
Costruire, in un fascio a punti limite, il cerchio ortogonale ad un dato cerchio di centro P.

Dati i punti limite L ed M ed il cerchio di centro P, per risolvere il problema teniamo conto che il cerchio che cerchiamo deve avere centro sulla retta LM ed essere ortogonale, oltreché al cerchio dato, ad un qualunque cerchio passante per L ed M (cioè del fascio ortogonale). Prendiamo dunque un qualunque cerchio per L ed M, di centro O' e troviamo l'asse radicale sua e del cerchio dato. Il cerchio che cerchiamo deve avere centro nel punto T di intersezione tra LM e quest'asse radicale. Per costruirlo basta ora condurre da T una delle due tangenti al cerchio dato. Nell'animazione si constata che in effetti la posizione di O' è ininfluente ai fini della determinazione di T.

Equazioni cartesiane

Se nel piano introduciamo un sistema di coordinate cartesiane ortogonali, allora un circolo ha equazione (canonica) del tipo

.

Se sono dati due circoli C₁ e C₂, una combinazione lineare con due coefficienti m ed n  non entrambi nulli è ancora l'equazione di una circonferenza (seppure, in generale, in forma non canonica): mC₁+nC₂=0. Per m=0 essa fornisce la circonferenza C₂, per n=0, la circonferenza C₁. Poiché i due parametri non possono essere entrambi nulli, l'equazione si può riscrivere con un solo parametro: , ove si è posto t=m/n. In questo caso si conviene che il circolo C₁ si ottenga per t=∞ (che corrisponde ad n=0).

Per t=-1 l'equazione precedente fornisce una retta che è l'asse radicale dei due circoli dati. La stessa retta è anche asse radicale di ogni altra coppia di circoli ottenuti per diversi valori di t: se ne deduce che l'insieme in questione è un fascio di circoli e i due circoli dati si chiamano circoli base.

Sono di immediata dimostrazione le seguenti proprietà, che abbiamo già incontrato con la definizione sintetica di fascio di circoli.

• Facendo la combinazione lineare di due qualunque circoli del fascio si ottiene ancora lo stesso fascio. Infatti: 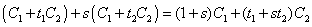, che è ancora una combinazione dei due circoli dati. In particolare il fascio si può ottenere per combinazione di un suo circolo qualunque e dell'asse radicale.
• Se i due circoli dati hanno due, uno, nessun punto in comune, allora la stessa proprietà vale per tutti i circoli del fascio che è detto, rispettivamente, un fascio ellittico, parabolico, iperbolico. Gli eventuali punti comune si dicono punti base del fascio. Se i due circoli dati sono concentrici allora tale è anche ogni altro circolo del fascio e l'asse radicale non risulta definita (è mandata all'infinito).
• Il centro di un generico circolo del fascio ha  le coordinate: 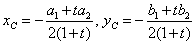. Se si elimina t si ottiene un'equazione di primo grado in x ed y, cioè una retta, che risulta essere perpendicolare all'asse radicale: è l'asse centrale.
• Il raggio di un generico circolo del fascio soddisfa la condizione 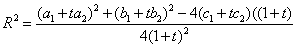, e quindi l'equazione R=0 ha al massimo due soluzioni: quando ci sono sono i punti limite, o di Poncelet, del fascio.
• Dalla equazione 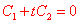si deduce subito C₁/C₂=-t. Questa condizione consente una facile dimostrazione della proprietà che ogni circolo del fascio è luogo dei punti che hanno potenze di rapporto costante rispetto ai due circoli C₁ e C₂.

Utilizzando le equazioni cartesiane si possono ritrovare, spesso in maniera più semplice, gli stessi risultati che si erano ottenuti per via puramente geometrica. L'approccio analitico, tuttavia, non si presta a valorizzare uno dei pregi didattici essenziali della geometria, che è costituito dalla sua accessibilità intuitiva, legata alle figure, alla visibilità. Le dimostrazioni, pur essendo in molti casi di gran lunga più semplici, sono per lo più verifiche di calcoli che non esercitano in alcun modo l'intuizione visiva. Si veda, a questo proposito, la nota di Benedetto Scimemi, Gruppi di trasformazioni geometriche, in Geometria e Multimedialità , Quaderno 35, Ministero Pubblica Istruzione, Liceo Vallisneri, Lucca, 1998-1999.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/12/2000 - ultimo aggiornamento il 01/12/2011