La divisione armonica di un segmento
Definizione di divisione armonica
Consideriamo, su una retta r, un segmento AB e due
punti C e D che dividono, internamente ed
esternamente, il segmento in parti aventi lo stesso rapporto:
.
I due punti C e D si dicono coniugati armonici in rapporto ad A e B. É immediato che se C e D sono coniugati armonici in rapporto ad A e B, allora A e B sono coniugati armonici in rapporto a C e D. La quaterna di punti (ABCD) costituisce una divisione armonica.
É chiaro che il valore comune dei due rapporti non può essere 1, perché D deve essere
esterno ad AB: se C è nel punto medio di AB non esiste
alcun D tale che ABCD sia una divisione armonica. Poiché
però all'avvicinarsi di C al punto medio di AB, D si
allontana all'infinito, si usa dire che il punto
all'infinito della retta r è il
coniugato armonico del centro del segmento AB.
Se il segmento AB si considera orientato e si prendono le misure
con segno dei segmenti orientati sopra la retta r,
orientata in un modo qualunque, la relazione che definisce i
punti C e D può essere riscritta così: 
o, equivalentemente, 
.
Costruzione geometrica
Se è dato il punto C si conduca una retta s per A, formante un qualunque angolo con la retta r (nel grafico è tracciata la perpendicolare), e su di essa si riportino C in C' e B in B'. Si costruisca, sempre su s, il simmetrico B'' di B' rispetto a C'. Si congiunga B'' con B e si tiri la parallela da C' a B''B: essa interseca r nel punto D richiesto (teorema di Talete). Costruzione quasi identica se è dato il punto D.
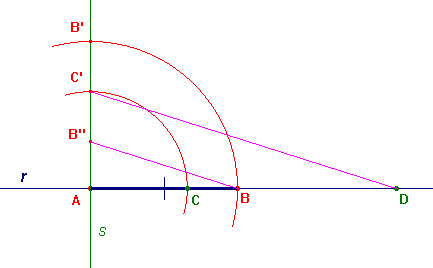
Si veda una costruzione dinamica con CabriJava.
Una costruzione molto simile è la seguente: da A si tracci una retta non coincidente con AB e su di essa si prenda un punto M. Si tracci, da B, la parallela ad AM e si indichi con P la sua intersezione con la retta MC. Se Q è il simmetrico di P rispetto al punto B, la retta MQ interseca la retta AB nel punto D cercato. Per la prova si sfrutti la similitudine tra i triangoli DBQ e DAM e poi tra i triangoli CPB e CAM, e si noti che PQ=QB.
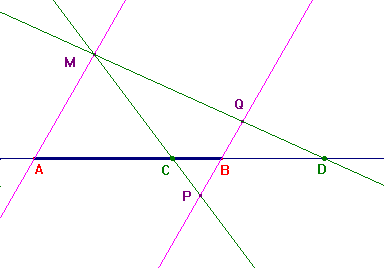
Si veda una costruzione dinamica con CabriJava.
Relazioni caratteristiche
Se si prende un sistema di ascisse sulla retta r, con
origine in A, e si indicano con a (che in questo caso
vale zero), b, c, d le ascisse dei
punti A, B, C, D, da si trova:
c(d-b)+d(c-b)=0; svolgendo i calcoli e dividendo per
bcd, si trova 
, ovvero 
.
Quest'ultima relazione mostra che AB è la media
armonica di AC e AD.
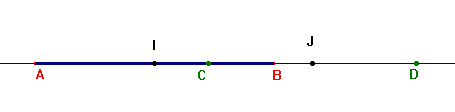
Se si prende un sistema di ascisse con l'origine nel punto medio, I, di AB si ottiene, con le stesse notazioni e osservando che b=-a, IA2=IB2=IC·ID. Analogamente se si prende come origine il punto medio, J, di CD si ottiene JC2=JD2=JA·JB. Queste due relazioni sono caratteristiche della divisione armonica.
Fasci armonici di rette
Si chiama fascio armonico un insieme di quattro rette condotte da un punto O ai quattro punti di una divisione armonica. Se il punto O è mandato all'infinito, le quattro rette risultano parallele e il fascio armonico è detto fascio armonico di rette parellele. Le rette del fascio si chiamano raggi.
Il teorema fondamentale sui fasci armonici è il seguente: Un fascio armonico determina una divisione armonica su qualunque retta secante i quattro raggi del fascio.
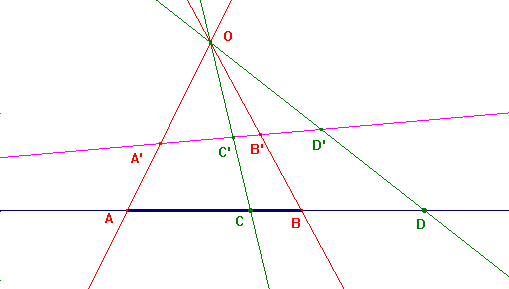
Se (ABCD) è una divisione armonica, anche (A'B'C'D') lo è, qualunque sia il punto O.
Esempi e applicazioni
1) Proprietà delle bisettrici in un triangolo
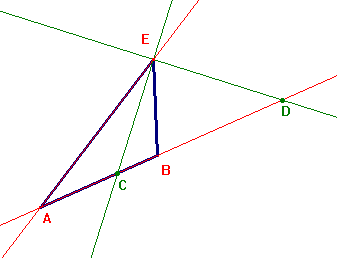
Se ABE è un triangolo e si conducono le due bisettrici degli angoli interno ed esterno in E, basta ricordare il teorema della bisettrice per concludere che (ABCD) è una divisione armonica.
2) Circonferenza di Apollonio
Il luogo dei punti M tali che il rapporto delle distanze da due
punti dati A e B è costantemente uguale a
k≠1 è una circonferenza che ha per
diametro i punti C e D della divisione armonica (ABCD)
caratterizzata dai rapporti =k. Questa
circonferenza è detta circonferenza di Apollonio.
Come è noto se invece k=1 il luogo in questione è l'asse del segmento AB.
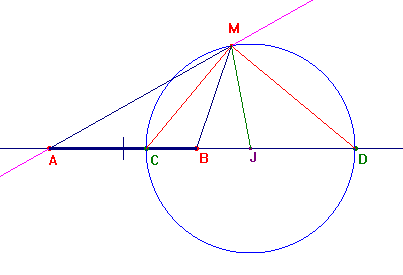
Infatti se M è un punto che soddisfa ai requisiti
richiesti esso sta su questo cerchio, perché le
bisettrici degli angoli AMB e del suo adiacente passano per C e
D e sono tra di loro perpendicolari. Inversamente, se M è
un punto del cerchio detto, si ha, come è noto,
JM2= JC2=JA·JB, da cui si deduce
che i triangoli JMA e JMB sono simili. Ne segue: 
.
Inoltre da 
si trae 
. Da
qui segue subito che 
.
Si veda un'animazione con CabriJava.