Proprietà dei coefficienti binomiali
I numeri 
godono di alcune interessanti
proprietà che qui vogliamo provare, anche come esempio di
calcoli tipici con questi coefficienti.
. Si tratta di una
proprietà che discende immediatamente dalla formula del
binomio di Newton. Infatti il primo membro rappresenta il
coefficiente di akbn-k, ovvero il
numero di volte che si deve scegliere a tra gli
n fattori del prodotto; è naturale che questo
stesso numero deve essere uguale al numero di volte che si deve
scegliere b tra gli stessi fattori, che è il
secondo membro. Si può comunque anche fare una
dimostrazione diretta. Si ha infatti:
.
. Basta applicare la
formula del binomio di Newton con a=b=1. Questa formula
ha un importante applicazione. Dato infatti un insieme
E di n elementi, il primo degli addendi a
secondo membro indica quanti sono i sottoinsiemi con zero
elementi (1 naturalmente, l'insieme vuoto!), il secondo
addendo indica quanti sono i sottoinsiemi con un elemento, ecc.
2n è dunque il numero dei
sottoinsiemi di un insieme con n elementi. Si veda una dimostrazione alternativa, basata
sulle disposizioni, dello stesso fatto.
. Anche qui basta
applicare la formula del binomio di Newton con a=1 e
b=-1.
Considerato un insieme E di
n elementi, fissiamo un suo elemento, diciamolo
a, e contiamo i sottoinsiemi di k elementi
separando, nel conteggio, quelli che contengono a da
quelli che non lo contengono. I primi sono
Cn-1,k-1, in quanto
basta scegliere k-1 elementi tra gli n-1
diversi da a e poi aggiungere a. I secondi
sono, ovviamente Cn-1,k.
Se ne deduce che 
. Questo risultato,
noto come Formula di Stifel (Michael Stifel, 1487-1567,
Arithmetica Integra), si poteva trarre anche per
calcolo diretto:
.
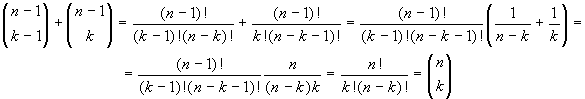E' questa la formula che sta alla base della costruzione del triangolo di Tartaglia. Basta scrivere una generica riga del triangolo e quella che la precede:
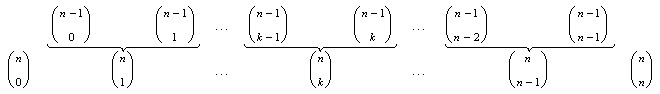
Consideriamo ora due insiemi A e
B, disgiunti e di cardinalità, rispettivamente,
n ed m. Se S è la loro unione,
Cn+m,k rappresenta il numero dei suoi
sottoinsiemi di k elementi. Questi sottoinsiemi si
costruiscono prendendo r elementi da A e i
restanti k-r da B, con r =
0,1,2,3,...,k. La scelta di r elementi da
A si può fare in Cn,r modi,
mentre la scelta di k-r elementi da B si
può fare in Cm,k-r modi; in totale la
scelta anzidetta si potrà dunque fare in
Cn,r·Cm,k-r modi.
Per avere il numero totale di sottoinsiemi basterà
sommare questi numeri per tutti i valori di r. Si
ottiene la seguente formula, detta Formula di convoluzione
di Vandermonde (Alexandre Theophile Vandermonde,
1735-1796):
, k ≤ min(n,m).
Una applicazione importante di questa
formula si ottiene ponendo n=m=k e tenendo conto che
:
.
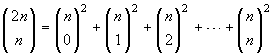Per ragioni di opportunità, in molte
circostanze, è utile estendere la definizione di anche al caso che n sia un numero reale
qualunque. Precisamente si pone: 
.
Si noti che, se n è un naturale minore di
k, si ha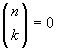 
, e inoltre che 
.