Disposizioni
Il problema che vogliamo affrontare è il seguente: Dato un insieme di n elementi in quanti modi è possibile costruire allineamenti ordinati di k di questi elementi?
Esempi
- Dati i simboli 1,2,X, quante colonne di 13 simboli siffatti si possono costruire? (Gioco del totocalcio).
- Dato un alfabeto di 26 simboli, quante sono le parole di tre simboli tutti distinti che si possono costruire (prescindendo dal significato!)?
- In una gara di Formula 1 con 20 piloti, quante sono le possibili terne candidate a salire sul podio?
Si noti che nel primo caso gli allineamenti richiesti comportano la possibilità di ripetizioni, negli altri due no.
Utilizzando lo schema a celle il problema può essere visualizzato così: Dati n simboli e k caselle numerate progressivamente, in quanti modi è possibile riempire le k caselle con gli n simboli?

E' chiaro che, se non sono consentite ripetizioni dei simboli, k non deve superare n, altrimenti non ci sono condizioni.
Utilizzando lo schema dell'urna il problema può invece essere visualizzato così: data un'urna con n palline numerate da 1 ad n, in quanti modi è possibile estrarre k palline a caso, tenendo conto dell'ordine di apparizione? L'estrazione senza reimbussolamento equivale a considerare allineamenti senza possibilità di ripetizione, quella con reimbussolamento consente invece le ripetizioni.
Se non sono previste ripetizioni il problema può essere anche riformulato in uno dei modi seguenti:
- Dato un insieme di n elementi quanti sono i suoi sottoinsiemi ordinati di k (≤n) elementi?
- Dati due insiemi, A di k elementi e B di n elementi, quante sono le funzioni iniettive di A in B?
Se sono previste ripetizioni il problema può essere anche riformulato nel seguente modo:
- Dati due insiemi, A di k elementi e B di n elementi, quante sono le funzioni di A in B?
L'interpretazione in termini di funzioni è particolarmente importante e si capisce subito se si pensa ad una funzione di questo tipo (cioè tra due insiemi finiti) come una tabella a doppia entrata: su una colonna (o riga) tutti gli elementi di A, sull'altra i corrispondenti elementi di B: se gli elementi di B non si possono ripetere si tratta di funzioni iniettive, altrimenti di funzioni generiche. Qui sotto sono proposti alcuni esempi, con A={1,2,3} e B={a,b,c,d}; i primi due rappresentano funzioni generiche, gli ultimi due funzioni iniettive.
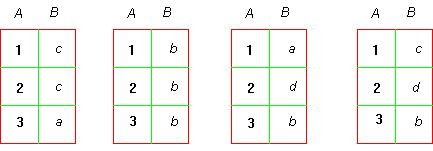
Si dà la seguente
Definizione
Dati due insiemi, A di k elementi e B di n elementi, una funzione iniettiva di A in B (o un sottoinsieme ordinato di B costituito da k elementi) si chiama una disposizione semplice di n oggetti a k a k, ovvero di classe k; una funzione (anche non iniettiva) di A in B si chiama invece una disposizione con ripetizione di n oggetti a k a k, ovvero di classe k.
Il numero delle disposizioni semplici di n oggetti di classe k si indica con Dn,k, quello delle disposizioni con ripetizione con Drn,k. E' immediato che valgono le seguenti formule:
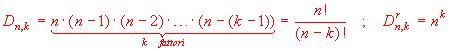
Per la dimostrazione basta solo osservare che se si devono riempire k caselline con n simboli, nella prima casellina si può mettere uno qualunque dei simboli (n possibilità di scelta), nella seconda uno dei rimanenti, se non sono consentite ripetizioni (n-1 possibilità di scelta), uno qualunque se sono consentite ripetizioni (ancora n possibilità di scelta).
La seconda delle formule dà origine ad un simbolo comunemente usato nello studio delle funzioni tra insiemi: l'insieme di tutte le funzioni da un insieme A in un insieme B si indica BA. Anzi, se α e β sono due numeri cardinali qualunque, rispettivamente riferiti ad un insieme A e ad un insieme B, si definisce la potenza βα come la cardinalità dell'insieme BA. Questa definizione nel caso di cardinali finiti riproduce la classica definizione di potenza, definizione che però viene estesa anche ai cardinali transfiniti. Un caso interessante si ha quando B è costituito da due soli elementi: se li chiamiamo true e false, si vede subito che il numero di queste funzioni è uguale al numero dei sottoinsiemi dell'insieme A. Se infatti ad un elemento di A corrisponde il valore true, esso starà nel corrispondente sottoinsieme, altrimenti no. Per esempio il sottoinsieme vuoto è quello che corrisponde alla funzione che ad ogni elemento di A fa corrispondere false. Per questo motivo si usa indicare con il simbolo 2A l'insieme delle parti di A, che avrà cardinalità 2α. Ques'ultima simbologia trova una giustificazione anche nel calcolo delle combinazioni di n oggetti di classe k.
Esempio
Dato A = {a,b,c,d}, le disposizioni semplici di classe 2 sono in numero D4,2 = 12, e sono: ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc. Le disposizioni con ripetizione della stessa classe sono invece Dr4,2 = 42 = 16, e sono le precedenti 12 con l'aggiunta di aa, bb, cc, dd.
Un problema di suddivisione
Lo schema a celle può anche essere visualizzato in un modo complementare rispetto a quello visto prima. Per considerare una disposizione di n oggetti di classe k si può immaginare di avere n celle (tante quanti sono gli oggetti) e k contrassegni che devono essere distribuiti tra le celle: se ogni cella ne può contenere al massimo uno si tratta di disposizioni senza ripetizione, se invece ne può contenere anche di più si tratta di disposizioni con ripetizione. I contrassegni corrispondono, nella sostanza, al posto che ciascun oggetto occupa nell'allineamento considerato all'inizio. Consideriamo per esempio le disposizioni di tre oggetti a due a due. Possiamo pensare di avere tre cassetti, denominati a, b, c, e due contrassegni, indicati con 1, 2, da piazzare nei tre cassetti:
| a | 1 | 2 | 1 | 2 | 1-2 | ||||
| b | 2 | 1 | 1 | 2 | 1-2 | ||||
| c | 2 | 1 | 2 | 1 | 1-2 |
Questo schema è utile per trattare problemi di suddivisione del tipo: avendo k oggetti tra di loro distinguibili, determinare in quanti modi è possibile suddividerli in n cassetti, tenendo conto di quali oggetti finiscono nei cassetti, mettendone al più uno per cassetto (disposizioni senza ripetizione) o consentendo un numero arbitrario di oggetti nei vari cassetti (disposizioni con ripetizione).
Riassumendo
Una disposizione di n oggetti di classe k si può realizzare con:
- Un'estrazione, che tenga conto dell'ordine, di k palline da un'urna contenente n palline distinguibili (con reimbussolamento se si accettano le ripetizioni, senza nel caso contrario).
- Un riempimento di k celle numerate progressivamente con n simboli diversi, con la possibilità che ciascun simbolo sia ripetuto più di una volta (disposizioni con ripetizione) oppure al massimo una volta (disposizioni semplici).
- Una distribuzione di k palline distinguibili in n celle (cassetti) diverse, con possibilità che ciascuna cella contenga anche più palline (disposizioni con ripetizione) oppure al massimo una pallina (disposizioni semplici).
Per esempio una colonna del totocalcio può essere vista:
- Come una successione di 13 estrazioni, con reimbussolamento, da un'urna contenente i simboli 1,X,2.
- Come il riempimento di 13 celle, numerate progressivamente, con i simboli 1,X,2.
- Come la sistemazione in tre cassetti, denominati 1,X,2, dei numeri da 1 a 13, essendo consentito che qualcuno dei cassetti possa restare vuoto.