Permutazioni
Permutazioni fra elementi distinti
Il caso in cui le disposizioni di n oggetti siano di classe n ha una particolare importanza, tanto da meritare un capitolo a sé nello studio del calcolo combinatorio. In questo caso si tratta di considerare le funzioni iniettive di un insieme in sé, oppure i possibili ordinamenti totali di un insieme di n elementi. In considerazione del fatto che gli insiemi che consideriamo sono finiti, ogni funzione iniettiva è anche biiettiva.
Si dà la seguente definizione.
Si chiama permutazione di un insieme A di n elementi una disposizione degli elementi di classe n.
Il numero Dn,n si indica anche con Pn e si ha, ovviamente,
Pn = n!
E' importante in molti esercizi, anche se praticamente ovvio, che n! = n·(n-1)! e, analogamente, n! = n·(n-1)·(n-2)!
Gli anagrammi di parole con lettere tutte distinte sono il più comune esempio di permutazioni. Negli anagrammi naturalmente hanno interesse anche quelli di parole formate da lettere non tutte distinte (come mamma). E' chiaro che in questo caso il numero di anagrammi è notevolmente inferiore rispetto a quello di parole con lo stesso numero di lettere tutte distinte: per esempio nel citato caso di mamma, uno scambio tra le m o tra le a non provoca cambiamenti nella parola. In questa e altre situazioni ha dunque interesse anche il calcolo del numero delle permutazioni, o allineamenti, su un insieme di oggetti non tutti distinti.
Permutazioni fra elementi non tutti distinti
Consideriamo allora un allineamento di n oggetti, di
cui n1 uguali ad un oggetto
a1, n2 uguali ad un
oggetto a2, ..., nk
uguali ad un oggetto ak, con
n=n1+n2+...+
nk. La determinazione del
possibile numero di allineamenti è immediata se si
suppone inizialmente che gli oggetti siano tutti distinti, si
calcola il numero delle loro possibili permutazioni
(n!) e si tiene conto che le ni!
permutazioni degli oggetti uguali ad ai non
danno luogo a situazioni distinte. Useremo il simbolo 
. Si può allora concludere con la seguente
formula:
La formula è valida anche per elementi tutti distinti, in cui si ha ni = 1, per ogni i. Poiché questi numeri sono legati allo sviluppo della potenza n-esima di un polinomio , si chiamano anche coefficienti polinomiali o multinomiali.
Esempi
Gli anagrammi della parola cane sono in numero di 4! = 24 e sono: cane, caen, cean, cena, cnae, cnea, aecn, aenc, anec, ance, acne, acen, eacn, eanc, ecan, ecna, enac, enca, nace, naec, neac, neca, ncae, ncea. Di questi solo quelli in corsivo hanno un significato nel vocabolario italiano.
Gli anagrammi della parola mamma sono in numero di 5!/(3!·2!) = 10 e sono: mamma, mmmaa, mmaam, mmama, mamam, ammma, amamm, aammm, ammam, amamm. Di questi solo l'originale ha un significato nel vocabolario italiano (d'altra parte si sa che di mamma ce n'é una sola!).
Ancora sulle permutazioni fra elementi non tutti distinti
Nello schema dell'urna il problema in considerazione equivale a considerare un'urna con n palline, di cui n1 del colore 1, n2 del colore 2, ..., nk del colore k. Si suppone che i colori siano distinguibili, ma le palline dello stesso colore no. Si tratta allora di considerare il numero di possibili estrazioni di tutte queste palline, senza reimbussolamento.
Per una ulteriore schematizzazione del problema nel modello a
celle, osserviamo che gli allineamenti di n oggetti, di
cui n1 del tipo 1, n2
del tipo 2, ..., nk del tipo k, si
possono realizzare nel seguente modo: date n celle,
scegliamo n1 posti dove sistemare gli
oggetti del primo tipo (e non conta l'ordine in cui li
sistemiamo, in quanto oggetti dello stesso tipo sono
indistinguibili), poi, tra le n-n1 celle
rimaste, scegliamo n2 posti in cui sistemare
gli oggetti del secondo tipo, e così via. Detto in altri
termini: dato un insieme di n elementi, consideriamo i
suoi sottoinsiemi di n1 elementi;
nell'insieme di n-n1 elementi rimasti
consideriamo i sottoinsiemi di n2 elementi,
e così via. Come vedremo studiamo le combinazioni, la prima scelta si può
fare in 
modi diversi, la seconda in 
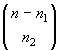modi diversi, e così via. Il numero totale di
possibilità è il prodotto di tutti questi fattori
e si ritrova, naturalmente, lo stesso risultato di prima.
Questo modo di schematizzare le permutazioni è utile per
risolvere un problema di ripartizione: in quanti modi n
oggetti distinti possono essere ripartiti in k
cassetti, in modo che nel primo ce ne vadano
n1, nel secondo n2, ecc.
(ovviamente in modo che si abbia sempre
n1+n2+...+nk
= n). La risposta è data da .
Riassumendo
Una permutazione di n oggetti, di cui n1 del tipo 1, n2 del tipo 2, ..., nk del tipo k (n1+n2+...+nk = n, con la possibilità che uno o più degli ni sia 1), si può vedere come:
- Un anagramma di una parola di n lettere, di cui n1 uguali ad una stessa lettera, n2 uguali ad una stessa lettera, e così via.
- Una ripartizione di n oggetti distinti in k cassetti, in modo che n1 vadano nel primo cassetto, n2 nel secondo cassetto, e così via.
- Un'estrazione di tutte le n palline contenute in un'urna, nell'ipotesi che ci siano n1 palline del colore 1, n2 palline del colore 2, ..., nk palline del colore k, e che le palline dello stesso colore siano indistinguibili, mentre i colori sono distinguibili.