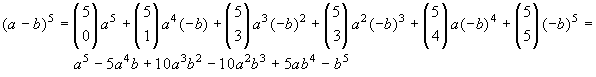La potenza del binomio
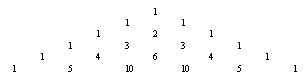Si vuole
calcolare (a+b)n. Il metodo studiato abitualmente nei primi anni di scuola
superiore si basa sulla costruzione del cosiddetto Triangolo di Tartaglia o di
Pascal. Il sistema è efficiente per piccoli valori di n, ma diventa pesante per
grandi valori, perché richiede la costruzione di tutte le righe precedenti l'ennesima, prima di
costruire l'ennesima. La formula che qui proporremo consente di superare questo ostacolo ed ha
anche altri usi importanti.
Consideriamo dunque la potenza (a+b)n, dove a e
b sono
reali e n è naturale. Per calcolare lo sviluppo si deve eseguire il prodotto:
(a+b)n = (a+b)·(a+b)·...·(a+b) (n volte).
E' ovvio che il risultato sarà costituito dalla somma di tanti monomi del tipo
akbn-k, con k compreso tra 0 ed n, con opportuni
coefficienti, per determinare i quali si tratta di contare quante volte compare ciascuno di questi
monomi. Il calcolo è facile se si tiene conto che basterà scegliere k volte il fattore
a tra gli n fattori, e di conseguenza n-k volte il fattore
b nei
rimanenti. Il numero cercato è allora (visto che l'ordine non conta!)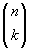 
.Otteniamo la formula:
Questa formula spiega perché il numero
si chiama coefficiente binomiale. La formula è nota con il nome di
Formula del binomio di Newton.
Esempio
