Gli enti fondamentali: punti, rette, semirette, segmenti, poligoni, angoli
Siamo ora pronti per addentrarci nel campo della geometria piana, cominciando ad introdurre assiomi, teoremi, definizioni. Dovremo preoccuparci di procedere rigorosamente con il metodo assiomatico-deduttivo, controllando sempre di utilizzare solo termini già definiti o affermazioni già provate. In realtà la cosa non è per niente semplice, ed è forse troppo ambiziosa per gli scopi che ci siamo prefissi: per questo abbiamo scelto la strada di iniziare a presentare la teoria nella forma più rigorosa possibile, con lo scopo di evidenziare le difficoltà che si presentano, per poi adottare un metodo "abbreviato" che ci consenta di giungere rapidamente ai risultati voluti.
L'impostazione che seguiremo prende le mosse da quella di Hilbert, con le necessarie semplificazioni e adattamenti: riteniamo importante che uno studente di Scuola Media Superiore abbia una conoscenza seppur parziale di una costruzione storicamente così importante. In ogni caso avvertiamo il lettore che questa pagina di introduzione degli enti fondamentali ha un aspetto "poco invitante", in quanto è infarcita di assiomi, piccoli teoremi, definizioni, ma non c'è scampo se vogliamo almeno cercare di far vedere come si inizia la costruzione di una teoria con le caratteristiche che ci siamo prefissi. Segnaliamo anche che alcuni degli assiomi non sarebbero strettamente necessari se ci si limita alla geometria del piano: li abbiamo comunque citati per questioni di completezza e per mantenere la numerazione originale di Hilbert.
ASSIOMA 1.1
Dati due punti distinti A e B esiste una retta r che li contiene.
ASSIOMA 1.2
Dati due punti distinti A e B esiste non più di una retta r che li contiene.
In sostanza dati due punti distinti A e B esiste una e una sola retta che li contiene. Questa retta si chiama anche retta AB, o retta BA. Diremo che i due punti individuano la retta. Diremo anche che la retta passa per i punti dati. Si usano anche espressioni come "la retta \(r\) passa per i due punti \(A\) e \(B\)", oppure "la retta \(r\) congiunge per i due punti \(A\) e \(B\)", ecc.
ASSIOMA 1.3
Una qualunque retta r contiene almeno due punti distinti. Esistono almeno tre punti che non stanno su una retta.
ASSIOMA 1.4
Dati tre punti A, B, C che non giacciono su una stessa retta, esiste un piano \(\alpha\) che contiene ciascuno dei tre punti A, B, C.
Si usano anche le espressioni "il punto \(A\) giace nel piano", "\(A\) è un punto del piano", ecc.
ASSIOMA 1.5
Dati tre punti .A, B, C che non giacciono su una stessa retta esiste non più di un piano che contiene i tre punti A, B, C.
ASSIOMA 1.6
Se due punti A e B di una retta appartengono ad un piano, allora tutti gli altri punti della retta appartengono al piano.
Questo assioma ci permetterà di limitare la nostra indagine ad un piano. D'ora in poi supporremo di lavorare in un determinato piano, senza avere bisogno di precisarlo.
ASSIOMA 1.7
Se due piani \(\alpha\) e \(\beta\) hanno un punto \(A\) in comune, allora essi hanno almeno un altro punto \(B\) in comune.
ASSIOMA 1.8
Esistono almeno quattro punti che non giacciono sullo stesso piano.
Per brevità punti che appartengono ad una stessa retta si dicono allineati o collineari.
Gli assiomi finora proposti si dicono anche assiomi di incidenza, in quanto si riferiscono a problemi di appartenenza reciproca di punti, rette e piani. Sono stati numerati seguendo la numerazione originale di Hilbert.
Teorema 1
Due rette distinte del piano hanno al massimo un punto in comune.
Visualizza la dimostrazione
Il teorema 1.1 lascia aperte due possibilità: date due rette distinte esse possono non avere punti in comune (attenzione: noi non sappiamo ancora se di coppie di rette di questo tipo ne esistono o no!), oppure hanno un sol punto in comune. Si dà allora la seguente definizione.
Definizione 1
Due rette distinte r ed s si dicono incidenti o concorrenti se hanno un solo punto in comune. Il punto comune si chiama punto di incidenza o di incontro delle rette.
Definizione 2
Due rette non incidenti si dicono parallele.
Sono di immediata dimostrazione i teoremi seguenti.
Teorema 2
Data una retta qualunque esiste almeno un punto che non le appartiene.
Teorema 3
Dato un punto qualunque esiste almeno una retta che non passa per il punto.
Teorema 4
Dato un punto qualunque esistono almeno due rette che passano per quel punto.
Teorema 5
Esistono tre rette che non passano per uno stesso punto.
Visualizza le dimostrazioni
Gli assiomi fin qui introdotti prefigurano una geometria molto povera, dove, per esempio, non è possibile garantire che dati due punti A e B e quindi una retta r, ci siano su r altri punti. Abbiamo bisogno di qualcos'altro per costruire il nostro modello di geometria del piano. Segnaliamo comunque che esistono, e hanno applicazioni interessanti, anche geometrie in cui il numero degli oggetti è finito. Chi fosse interessato può vederne una semplice introduzione nell'apposita pagina sulle geometrie finite.
ASSIOMA 2.1
Se un punto B giace tra un punto A e un punto C, allora i punti A, B, C sono tre punti distinti di una retta e B giace anche tra C ed A.
ASSIOMA 2.2
Dati due punti qualunque A e C, esiste almeno un punto B sulla retta AC tale che C sta tra A e B.

Questo assioma è, nella sostanza, quello che ci permette di "prolungare" indefinitamente un segmento.
ASSIOMA 2.3
Dati tre punti distinti di una retta, allora al più uno dei tre sta tra gli altri due.
Questi assiomi ci consentono di introdurre l'importante concetto di segmento mediante la seguente
Definizione 3
Si chiama segmento aperto ]A,B[ l'insieme di tutti i punti che stanno tra A e B. Si chiama segmento chiuso, o semplicemente segmento [A,B], il segmento aperto a cui si aggiungano i punti A e B. Il segmento (chiuso) si indica anche con AB.
Si noti che abbiamo usato lo stesso simbolo AB sia per indicare una retta che per indicare un segmento. Il contesto renderà chiaro di quale dei due concetti si vuol parlare. I punti del segmento AB distinti da A e B si dicono interni al segmento, A e B si dicono estremi del segmento. I punti della retta AB che non stanno sul segmento AB si dicono esterni al segmento. Si usa chiamare segmento nullo un segmento in cui i due punti A e B coincidono. Notiamo esplicitamente che, fissati due punti A e B, si ha AB = BA.
ASSIOMA 2.4 (di Pasch)
Siano A, B, C tre punti non allineati e sia r una retta del piano che non passa per nessuno dei tre punti dati. Se la retta r passa per un punto del segmento AB, passa anche per un punto del segmento AC oppure per un punto del segmento BC.
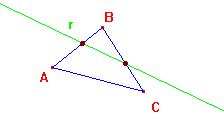 Questo assioma, la cui
interpretazione geometrica è indicata nella figura qui a
lato, non è inserito da Euclide tra i suoi postulati,
anche se viene regolarmente utilizzato fin nelle prime pagine
degli Elementi. Il suo enunciato potrà essere (al momento
opportuno, cioè quando si sarà introdotto il
concetto di triangolo) semplificato in: se una retta entra
in un triangolo attraversando un lato deve necessariamente
uscirne attraversando un altro lato. In effetti
l'evidenza "sperimentale" di questo fatto è
talmente forte, che è difficile pensare alla
necessità di postularlo esplicitamente. Fu Moritz Pasch,
nel 1882, ad accorgersi per primo della impossibilità di
dedurre questo fatto come conseguenza degli altri assiomi. Lo
stesso Pasch si accorse anche di altri assiomi implicitamente
assunti, ma non dichiarati, da Euclide. Segnaliamo il fatto che,
secondo lo storico di matematica araba Adolf Youschkevitch
(Les mathématiques arabes du VIIIè au
XVè siècle, Vrin-CNRS, Parigi, 1976), questa
scoperta è dovuta a Ibn al Haytham, più noto in
Europa con il nome di Alhazen e vissuto tra il 965 circa e il
1039, quindi molto prima di Pasch. In realtà nella nostra
cultura matematica "grecocentrica", il contributo
delle altre civiltà è spesso sottovalutato, per
non dire ignorato. Chi è interessato a questo argomento
può leggere qualche osservazione nella pagina su Matematica ed eurocentrismo.
Questo assioma, la cui
interpretazione geometrica è indicata nella figura qui a
lato, non è inserito da Euclide tra i suoi postulati,
anche se viene regolarmente utilizzato fin nelle prime pagine
degli Elementi. Il suo enunciato potrà essere (al momento
opportuno, cioè quando si sarà introdotto il
concetto di triangolo) semplificato in: se una retta entra
in un triangolo attraversando un lato deve necessariamente
uscirne attraversando un altro lato. In effetti
l'evidenza "sperimentale" di questo fatto è
talmente forte, che è difficile pensare alla
necessità di postularlo esplicitamente. Fu Moritz Pasch,
nel 1882, ad accorgersi per primo della impossibilità di
dedurre questo fatto come conseguenza degli altri assiomi. Lo
stesso Pasch si accorse anche di altri assiomi implicitamente
assunti, ma non dichiarati, da Euclide. Segnaliamo il fatto che,
secondo lo storico di matematica araba Adolf Youschkevitch
(Les mathématiques arabes du VIIIè au
XVè siècle, Vrin-CNRS, Parigi, 1976), questa
scoperta è dovuta a Ibn al Haytham, più noto in
Europa con il nome di Alhazen e vissuto tra il 965 circa e il
1039, quindi molto prima di Pasch. In realtà nella nostra
cultura matematica "grecocentrica", il contributo
delle altre civiltà è spesso sottovalutato, per
non dire ignorato. Chi è interessato a questo argomento
può leggere qualche osservazione nella pagina su Matematica ed eurocentrismo.
Gli assiomi 2.1, 2.2, 2.3, 2.4 si dicono anche assiomi di ordine (betweenness axioms), per evidenti motivi. Hilbert per questi assiomi rimanda esplicitamente a Pasch, che ne aveva fatto uno studio sistematico.
Una prima conseguenza fondamentale di questi assiomi è il fatto che i segmenti non sono vuoti. Come si vedrà la dimostrazione di questo teorema richiede l'uso di tutti gli assiomi introdotti, in particolare quello di Pasch e, con gli strumenti di cui disponiamo, non è per niente banale.
Teorema 6
Dati due punti A e C, il segmento AC contiene punti diversi da A e C, ovvero il segmento aperto ]A,C[ non è vuoto.
Visualizza la dimostrazione
 Nonostante le
apparenze, questo teorema non ci consente di concludere subito
che tra A e C esistono infiniti punti. E'
ben vero che, iterando il procedimento, una volta trovato un
punto D tra A e C, si può
trovare un punto M tra A e D (e poi
si può procedere in maniera simile), ma non è
ancora detto che esso stia anche tra A e C,
come l'intuizione suggerisce: dovremmo dimostrarlo.
Nonostante le
apparenze, questo teorema non ci consente di concludere subito
che tra A e C esistono infiniti punti. E'
ben vero che, iterando il procedimento, una volta trovato un
punto D tra A e C, si può
trovare un punto M tra A e D (e poi
si può procedere in maniera simile), ma non è
ancora detto che esso stia anche tra A e C,
come l'intuizione suggerisce: dovremmo dimostrarlo.
Questa osservazione è abbastanza interessante e costituisce una riprova di quanto sia delicata l'introduzione in forma assiomatica dei principi della geometria. Per gli scopi che ci siamo prefissi, comunque, non potremo ulteriormente seguire in maniera sistematica l'approccio di Hilbert e cominceremo ad operare drastiche semplificazioni, in particolare raccogliendo alcuni risultati in teoremi di cui non forniamo la dimostrazione e sottintendendo alcuni altri risultati particolarmente intuitivi.
Teorema 7
- Se tre punti A, B, C stanno su una stessa retta, esattamente uno di essi si trova tra gli altri due.
- Dati quattro punti su una retta è sempre possibile
assegnare ad essi i nomi A, B, C, D, in modo tale che
B stia tra A e C e anche tra
A e D, e che C stia tra B e
D e anche tra A e D. ![]() .
.
- Dati due punti su una retta, tra essi esiste un numero infinito di punti.
- Data una qualunque retta r e un punto P su di essa, il punto P individua sulla retta tre classi: il punto P stesso e due sottoinsiemi che chiamiamo semirette di origine P, con la proprietà che P appartiene ad entrambe e che se A e B sono due punti, uno su una semiretta e uno sull'altra, il punto P sta sul segmento AB.
- Ogni retta r individua nel piano tre classi: la retta r stessa e due sottoinsiemi che chiamiamo semipiani con retta origine r, con la proprietà che r appartiene ad entrambi e che se A e B sono due punti, uno su un semipiano e uno sull'altro, il segmento AB interseca la retta r, se invece i due punti A e B sono nello stesso semipiano, il segmento AB non interseca la retta r.
E' ora possibile anche parlare di ordinamento sulla retta:
tra i punti di una retta si può stabilire una relazione
di ordine stretto,![]() ,
che definisce un verso di
percorrenza sulla retta. I possibili versi di percorrenza
sono due, detti opposti. Stabilito
uno dei due versi, la retta si dice orientata. Le due semirette individuate da un
punto P su una retta possono anche essere pensate come
l'insieme dei punti che precedono o seguono P
nell'ordine scelto: esse si dicono anche semirette adiacenti. Si possono anche
considerare semirette aventi l'origine in comune, ma
appartenenti a rette diverse: si diranno semirette consecutive.
,
che definisce un verso di
percorrenza sulla retta. I possibili versi di percorrenza
sono due, detti opposti. Stabilito
uno dei due versi, la retta si dice orientata. Le due semirette individuate da un
punto P su una retta possono anche essere pensate come
l'insieme dei punti che precedono o seguono P
nell'ordine scelto: esse si dicono anche semirette adiacenti. Si possono anche
considerare semirette aventi l'origine in comune, ma
appartenenti a rette diverse: si diranno semirette consecutive.
Dato un segmento AB si possono considerare due semirette: una di origine A e contenente B e una di origine B e contenente A. Esse si chiamano prolungamenti di AB, rispettivamente dalla parte di B e dalla parte di A. Due segmenti aventi solo un estremo in comune si dicono consecutivi; se essi stanno su una stessa retta si dicono adiacenti.
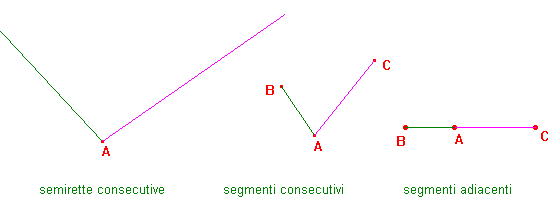
Definizione 4
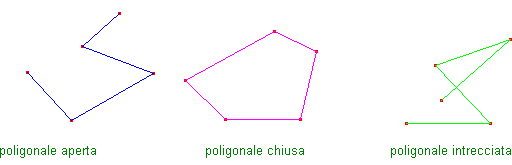
Più segmenti AB, BC, CD, ... , a due a due consecutivi e non adiacenti costituiscono una poligonale. I segmenti si dicono lati della poligonale, i loro estremi si dicono vertici, il primo estremo del primo segmento e il secondo dell'ultimo si chiamano estremi della poligonale. Se gli estremi coincidono la poligonale si dice chiusa, altrimenti aperta. Una poligonale chiusa si chiama anche poligono. Se due lati non consecutivi hanno un punto in comune, la poligonale si dice intrecciata. Una poligonale chiusa con tre lati si chiama un triangolo, con quattro lati un quadrilatero, ecc.
Definizione 5
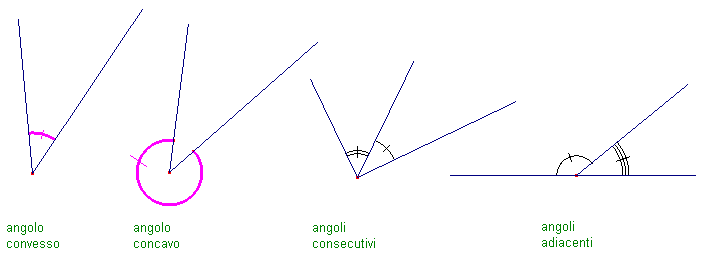
Date due semirette distinte del piano, aventi l'origine in comune, si chiama angolo ciascuno dei due sottoinsiemi disgiunti del piano individuati dalle due semirette, unito con le semirette stesse.
Se le due semirette sono adiacenti, ciascuno dei due angoli si chiama piatto. Se le semirette non sono adiacenti si chiama angolo convesso quella delle due parti che contiene tutti i segmenti che hanno un estremo su una semiretta e l'altro sull'altra, si chiama invece angolo concavo l'altra parte. Per estensione, se le due semirette coincidono, si chiama angolo giro l'intero piano, angolo nullo l'insieme vuoto. L'origine comune delle due semirette si chiama vertice dell'angolo, le due semirette si chiamano lati.
Due angoli che hanno il vertice e un lato in comune e gli altri due lati appartenenti ciascuno ad uno dei due semipiani opposti, individuati dalla retta che contiene il lato comune, si chiamano consecutivi. Due angoli consecutivi si dicono adiacenti se i lati non in comune stanno su semirette adiacenti.
Gli angoli possono essere indicati mediante la coppia,
r ed s, di semirette che lo individuano (![]() (r,s)) o mediante la scelta di un punto
(B,C) su ciascuna delle due semirette che lo
individuano e il vertice (A) (
(r,s)) o mediante la scelta di un punto
(B,C) su ciascuna delle due semirette che lo
individuano e il vertice (A) (![]() BÂC o anche BÂC, o ancora
più semplicemente BAC se non c'è
possibilità di equivoco). In molti casi gli angoli sono
anche indicati con le lettere dell'alfabeto greco: α,
β, ...
BÂC o anche BÂC, o ancora
più semplicemente BAC se non c'è
possibilità di equivoco). In molti casi gli angoli sono
anche indicati con le lettere dell'alfabeto greco: α,
β, ...
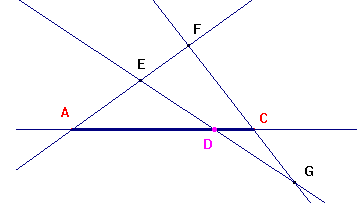 Dati i punti A e C, esiste almeno
un punto E esterno alla retta AC. Esistono
poi un punto F su AE, esterno al segmento
AE, e un punto G su FC, esterno al
segmento FC.
Dati i punti A e C, esiste almeno
un punto E esterno alla retta AC. Esistono
poi un punto F su AE, esterno al segmento
AE, e un punto G su FC, esterno al
segmento FC.