Geometrie finite - Il metodo assiomatico
Le geometrie finite descrivono un sistema di oggetti (che chiamiamo sempre punti o rette) con la caratteristica peculiare di essere finito. La geometria di Euclide non è finita, perché ogni retta, per esempio, contiene infiniti punti. Lo studio delle geometrie finite ha assunto in tempi recenti grande importanza, anche per i suoi legami con l'analisi combinatoria e per numerose altre applicazioni. Uno dei padri di questi studi è Gino Fano, esponente di grande rilievo della scuola italiana di geometria algebrica che tra la fine dell'Ottocento e i primi decenni del Novecento ha dominato il panorama internazionale delle ricerche geometriche.
E' significativo notare come si possa costruire una teoria assiomatica che usi gli stessi concetti della ordinaria geometria, anche in situazioni in cui gli oggetti da trattare sono in numero finito. E' chiaro che l'idea fisica di punto o di retta che ci si fa in geometrie di questo tipo non potrà coincidere con quella che scaturisce dagli assiomi, spesso identici, che si utilizzano per la geometria ordinaria (o anche per le geometrie non euclidee). E' proprio questo uno dei principali motivi che ci hanno spinto ad inserire un breve cenno di questi concetti nel nostro corso: mostrare su esempi concreti (e semplici, in quanto gli insiemi finiti sono più "abbordabili" di quelli infiniti) come nella costruzione della geometria siano fondamentali gli assiomi più che le rappresentazioni visive che noi ci facciamo degli oggetti.
Sia per capire bene l'idea di geometria finita, che per riassumere e sistemare concetti trattati in varie parti di questo corso di geometria, richiamiamo qui, molto schematicamente, le principali caratteristiche dei sistemi di assiomi.
Il metodo assiomatico
Il metodo assiomatico consiste di:
- Un insieme di termini tecnici che non vengono definiti e che il lettore interpreta opportunamente: si tratta dei termini non definiti o degli enti primitivi..
- Un ulteriore insieme di termini tecnici definiti utilizzando i termini indefiniti: si tratta delle definizioni del sistema.
- Un insieme di affermazioni che riguardano i termini indefiniti e di definizioni che non vengono provate: si tratta degli assiomi del sistema.
- Un ulteriore insieme di affermazioni che devono essere logiche conseguenze degli assiomi: si tratta dei teoremi del sistema. Una prova è il risultato di una successione di affermazioni, ciascuna della quali segue logicamente da quelle precedenti e che conduce da una proposizione che si sa essere vera ad un'altra che deve essere provata.
Dando ad ognuno dei termini non definiti un particolare significato, si costruisce una interpretazione del sistema. Se per una data interpretazione e del sistema, tutti gli assiomi sono veri, quella interpretazione si chiama un modello. Esempi di modelli sono quelli di Klein e di Poincaré delle geometrie non euclidee. Ci possono essere sostanzialmente due tipi di modelli:
- Modelli concreti: gli enti primitivi sono rappresentati con oggetti del mondo fisico (magari idealizzati).
- Modelli astratti: gli enti primitivi sono rappresentati con oggetti presi da altri sistemi assiomatici, come per esempio i numeri reali.
Proprietà dei sistemi assiomatici
![]() Compatibilità . Un insieme
di assiomi è compatibile se è impossibile dedurre
da essi un teorema che contraddice gli assiomi o un teorema
già provato. Si può anche dire, in maniera
equivalente, che un sistema è incompatibile se implica
una contraddizione, cioè se esiste una proposizione
contemporaneamente vera e falsa.
Compatibilità . Un insieme
di assiomi è compatibile se è impossibile dedurre
da essi un teorema che contraddice gli assiomi o un teorema
già provato. Si può anche dire, in maniera
equivalente, che un sistema è incompatibile se implica
una contraddizione, cioè se esiste una proposizione
contemporaneamente vera e falsa.
Un esempio di sistema incompatibile:
- A1. Ci sono esattamente due ragazzi.
- A2. Ci sono esattamente tre ragazze.
- A3. Ogni ragazzo ama esattamente due ragazze.
- A4. Nessuna coppia di ragazzi ama la stessa ragazza.
Un modo per provare la compatibilità di un sistema di assiomi è di costruire un modello concreto (in questo caso si parla di compatibilità assoluta) o astratto (in questo caso si parla di compatibilità relativa).
![]() Indipendenza. Un assioma è
indipendente se non è una logica conseguenza degli altri.
Un sistema di assiomi è indipendente se ogni assioma
è indipendente.
Indipendenza. Un assioma è
indipendente se non è una logica conseguenza degli altri.
Un sistema di assiomi è indipendente se ogni assioma
è indipendente.
Un modo per provare che un assioma è indipendente è quello di costruire un modello in cui l'assioma è falso mentre gli altri sono veri.
![]() Completezza. Un sistema di
assiomi è completo se è impossibile aggiungere
ulteriori assiomi senza introdurre altri termini non definiti.
Completezza. Un sistema di
assiomi è completo se è impossibile aggiungere
ulteriori assiomi senza introdurre altri termini non definiti.
Le verifiche di compatibilità, indipendenza e completezza sono spesso molto complesse. L'esempio più eclatante è dato dalla geometria di Euclide: la verifica della indipendenza degli assiomi (in particolare dell'assioma delle parallele) ha richiesto molti secoli di discussione.
Le geometrie finite
Affinché una configurazione di punti e linee sia considerata una geometria finita devono essere verificate alcune proprietà generali, che si possono riassumere nel seguente schema.
- Il numero di punti è finito.
- Il numero di linee è finito.
- Ogni linea contiene lo stesso numero di punti (≥2).
- Ogni punto appartiene allo stesso numero di linee (≥2).
- Ogni coppia di punti distinti sta al più su una linea.
- Ogni coppia di linee distinte si interseca su al più un punto.
- Non tutti i punti stanno su una stessa linea.
- C'è almeno una linea.
Per questioni di semplicità di linguaggio anziché dire "un punto sta su una linea" e "una linea passa per un punto", si usa la stessa locuzione in entrambi i casi: "un punto sta su una linea" e "una linea sta su un punto". Si noti che nella geometria di Euclide valgono le proprietà dalla 3 alla 7, in particolare la 3 (ogni linea contiene infiniti punti) e la 4 (ogni punto appartiene a infinite rette, quelle del fascio proprio da esso individuato).
La geometria dei quattro punti
I termini primitivi sono punto, linea, su.
Gli assiomi sono:
- A1. Ci sono esattamente quattro punti.
- A2. Due punti distinti hanno esattamente una linea su entrambi.
- A3. Ogni linea è esattamente su due punti.
I teoremi chiave in questa geometria sono:
- Nella geometria dei quattro punti ci sono esattamente sei linee.
- Nella geometria dei quattro punti ogni linea ha esattamente una linea ad essa parallela.
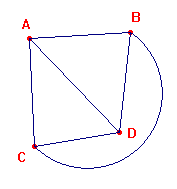 Un possibile modello è quello rappresentato qui a fianco,
dove i punti sono A, B, C, D, e le linee sono AB,
CD, BC, AD, BD, AC.
Un possibile modello è quello rappresentato qui a fianco,
dove i punti sono A, B, C, D, e le linee sono AB,
CD, BC, AD, BD, AC.
Si tenga presente che le linee devono essere pensate solo come sottoinsiemi dell'insieme dei punti e i segmenti o archi che abbiamo usato servono solo a evidenziare questi sottoinsiemi.
E' chiaro che le coppie di linee AB - CD, AD - BC, AC - BD, sono parallele, in quanto non hanno punti in comune; é altresì immediato verificare che gli assiomi indicati sono verificati.
La scelta di rappresentare la sesta linea come un arco è solo legata al desiderio di non far intersecare nemmeno visivamente AD con BC: in realtà in questa geometria le linee possono essere pensate come "diritte" nel senso ordinario.
Un possibile modello concreto di questa geometria è il seguente: Quattro studenti vogliono giocare al computer uno contro l'altro e vogliono connettere i computer con cavi (non con una connessione di rete mediante server). Nella figura di sopra i punti rappresentano i computer e le linee i cavi. Anche se questa situazione può essere considerata banale, essa fa vedere quale tipo di applicazioni possono essere derivate dai modelli di geometria finita. E' chiaro, in questo modello, che i cavi possono essere tranquillamente pensati "diritti", in accordo con quanto abbiamo detto sopra riguardo al modello astratto.
La geometria di Fano
I termini primitivi sono punto, linea, su.
Gli assiomi sono:
- A1. Esiste almeno una linea.
- A2. Ci sono esattamente tre punti su ogni linea.
- A3. Non tutti i punti stanno su una stessa linea.
- A4. C'è esattamente una linea su due punti distinti.
- A5. C'è almeno un punto su ogni due linee distinte.
I teoremi chiave in questa geometria sono:
- Nella geometria di Fano due linee qualunque hanno esattamente un punto in comune (questo significa che non esistono linee parallele ad una linea data).
- Nella geometria di Fano ci sono esattamente sette punti e sette linee.
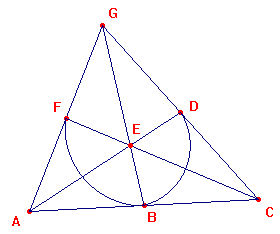 Un
possibile modello astratto di questa geometria è
rappresentato qui a lato. Si noti come sei delle sette linee
possono essere pensate come "diritte" nel senso
ordinario del termine, mentre la settima no. In questa
geometria, inoltre, non esistono linee parallele ad una data
linea.
Un
possibile modello astratto di questa geometria è
rappresentato qui a lato. Si noti come sei delle sette linee
possono essere pensate come "diritte" nel senso
ordinario del termine, mentre la settima no. In questa
geometria, inoltre, non esistono linee parallele ad una data
linea.
Ci sono parecchi modelli concreti di uso comune di questa geometria. Ne proponiamo due.
Primo modello - In un parlamento di sette persone si vogliono costituire sette commissioni di tre persone ciascuna, in modo che ogni persona partecipi a tre commissioni, che due commissioni abbiano almeno un membro in comune e che una determinata coppia di persone partecipi ad una sola commissione. Se identifichiamo i parlamentari con punti e le commissioni con linee, il modello di Fano risolve esattamente questo problema.
Secondo modello - Una rete per comunicazioni mediante switch box. In una rete di questo tipo si vuole che
- Due utenti qualunque siano connessi ad uno switch.
- Tutti gli switch devono essere utilizzati con lo stesso carico.
- Deve essere usato il minor numero possibile di switch (più di uno comunque).
Se chiediamo che ciascuno switch connetta esattamente tre utenti e pensiamo gli utenti come punti, e gli switch come linee, il modello di Fano risolve esattamente questo problema.
I due esempi di reti di comunicazione che abbiamo proposto non sono casuali: in questo campo le applicazioni delle geometrie finite sono all'ordine del giorno (anche se spesso non sono così semplici!).