Il modello di Klein della geometria iperbolica
Le geometrie non euclidee possono essere rappresentate utilizzando modelli che si basano sulle ordinarie figure della geometria euclidea. Questo ci consente di avere una idea visiva di come vanno le cose in queste geometrie, anche se in genere una trattazione esplicita delle varie proprietà è abbastanza difficile. In questa e nelle analoghe pagine in cui proponiamo modelli di geometrie non euclidee vogliamo solo accennare al problema, senza entrare nei dettagli: scopo principale è quello di stimolare la curiosità del lettore. Per approfondimenti rimandiamo alla letture e ai siti citati in bibliografia.
Il modello di Klein è tra i più semplici della geometria iperbolica. Si tratta di un modello di questa geometria in cui i concetti di punto, retta, piano, non hanno una rappresentazione granché diversa rispetto a quanto siamo abituati nella geometria di Euclide. La cosa radicalmente diversa è costituita dal fatto che non vale il postulato delle parallele nella forma di Euclide.
Consideriamo un cerchio, che indichiamo con K, e diamo le seguenti definizioni:
- Punto è un punto interno (sono cioè esclusi i punti sul bordo).
- Retta è una qualunque corda, privata degli estremi.
- Piano è l'insieme di tutti i punti interni.
 E'
immediato verificare che, in questo modello, per due punti passa
una sola retta, che esistono almeno tre punti distinti che non
stanno su una stessa retta, e altri assiomi validi nella
ordinaria geometria di Euclide.
E'
immediato verificare che, in questo modello, per due punti passa
una sola retta, che esistono almeno tre punti distinti che non
stanno su una stessa retta, e altri assiomi validi nella
ordinaria geometria di Euclide.
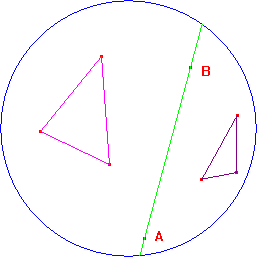
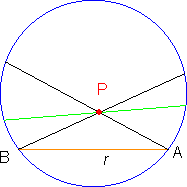
Però se si considera una retta r ed un punto P fuori di essa, per P passano infinite rette che non intersecano r. Nella figura a lato abbiamo tracciato le due rette "limite", PA e PB che non intersecano r, perché i punti A e B della circonferenza non fanno parte del nostro "piano", ed un altra retta intermedia, anch'essa senza intersezioni con r. Le rette PA e PB sono considerate parallele ad r, mentre le altre sono considerate "non secanti" o "ultraparallele" (è più che altro una questione di definizioni: nel senso usuale potrebbero tranquillamente essere definite parallele).
Una geometria come questa è stata definita iperbolica da F.Klein perché in greco iperbole significa eccesso, in relazione al fatto che il numero di parallele è in eccesso rispetto a quanto previsto dalla geometria di Euclide.
Questo modello, seppure molto semplice da definire, presenta però una serie di problemi, in particolare con la definizione di angolo: gli angoli nel modello non sono definiti allo stesso modo che nel piano euclideo.
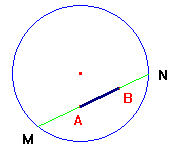 Naturalmente c'è anche il problema di una
definizione di distanza che, tra l'altro, renda le rette
infinitamente lunghe. Questa definizione richiede l'uso dei
logaritmi e si dà nel seguente modo: considerato il
segmento AB, lo si prolunga (in una retta) fino ad
incontrare in M ed N la circonferenza limite
del nostro piano di Klein. Si pone poi
Naturalmente c'è anche il problema di una
definizione di distanza che, tra l'altro, renda le rette
infinitamente lunghe. Questa definizione richiede l'uso dei
logaritmi e si dà nel seguente modo: considerato il
segmento AB, lo si prolunga (in una retta) fino ad
incontrare in M ed N la circonferenza limite
del nostro piano di Klein. Si pone poi ![]() . Sfruttando le proprietà dei logaritmi si
vede subito che se A e B coincidono la
distanza diventa zero, mentre se uno dei due punti si avvicina
al bordo del cerchio la distanza diventa infinita. Questa
definizione di lunghezza soddisfa anche i requisiti normali che
una lunghezza deve avere, e cioè è sempre positiva
ed è additiva (se un segmento è l'unione di
due segmenti la sua lunghezza è la somma delle due
lunghezze).
. Sfruttando le proprietà dei logaritmi si
vede subito che se A e B coincidono la
distanza diventa zero, mentre se uno dei due punti si avvicina
al bordo del cerchio la distanza diventa infinita. Questa
definizione di lunghezza soddisfa anche i requisiti normali che
una lunghezza deve avere, e cioè è sempre positiva
ed è additiva (se un segmento è l'unione di
due segmenti la sua lunghezza è la somma delle due
lunghezze).
Un modello simile a quello di Klein, ma in cui la definizione di angolo è identica a quella usuale è il modello di Poincaré.
La trattazione del modello di Klein non è semplice, ma ci può venire in aiuto il solito Cabri che, con un menu opportuno, ci consente di costruire automaticamente le principali figure della geometria. Tra le tante versioni di questo menu segnaliamo quella che si può reperire, con le istruzioni per l'uso (in inglese!), su http://www.gettysburg.edu/~dflesner/.
Nelle figure che seguono proponiamo alcune costruzioni, realizzate con il Cabri-menu sopra citato, con qualche commento.
|
Due triangoli simmetrici rispetto ad una retta AB. |
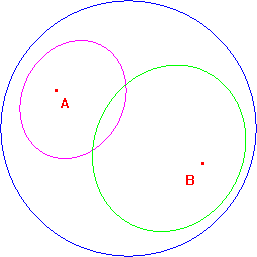
Due cerchi di centri A e B rispettivamente. |
|
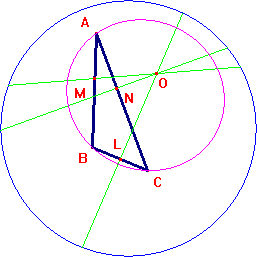
Un triangolo, gli assi dei tre lati e il cerchio circoscritto (L, M, N sono i punti medi dei tre lati). |
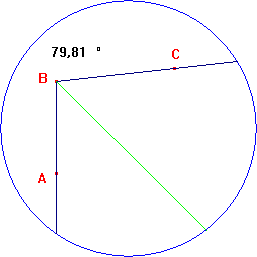
Un angolo, la sua bisettrice e la sua misura. |
|
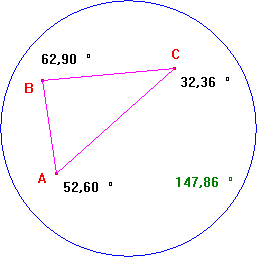
Un triangolo, la misura dei suoi angoli, e la loro somma (minore di 180° come deve essere in questa geometria). |
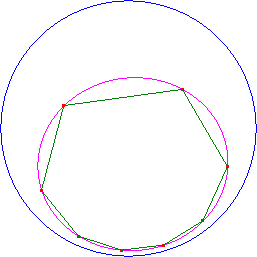
Un ottagono regolare e il cerchio ad esso circoscritto. |
|
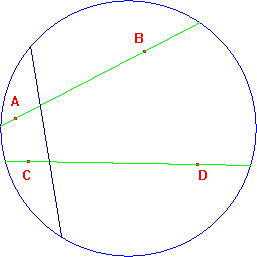
Due rette AB e CD ultraparallele e l'unica perpendicolare comune ad esse. |
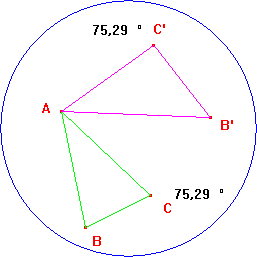
Un triangolo ABC e lo stesso ruotato di 70° nella posizione AB'C'; sono riportate, per controllo, le misure degli angoli in C e C', ovviamente uguali. |