Congruenza
Il concetto di congruenza viene assunto da Hilbert come primitivo. Gli assiomi relativi rendono formalmente preciso il concetto di "uguaglianza mediante movimento rigido" utilizzato da Euclide: Cose che si possono sovrapporre una con l'altra sono uguali.
Il concetto di congruenza ci permetterà di introdurre, per esempio, il concetto di punto medio di un segmento, in altre parole ci consentirà, in un certo senso, di "organizzare" i punti di un segmento. Discorso simile per gli angoli, dove saremo autorizzati ad introdurre il concetto di bisettrice. Segnaliamo esplicitamente che, in molti testi (e lo riconosce anche il Syllabus di matematica dell'UMI), si usa la parola "uguale" al posto di "congruente".
ASSIOMA 3.1
Se A e B sono due punti su una retta r e A' è un punto sulla stessa retta o su un'altra retta r', allora è sempre possibile trovare un punto B' da una parte della retta r (o r') tale che AB e A'B' siano congruenti. In formule AB ≡ A'B'.
Detto in altri termini: si possono trasportare rigidamente i segmenti, senza alterarne le caratteristiche.
ASSIOMA 3.2
Se A'B' e A"B" sono congruenti ad un stesso segmento AB, allora sono congruenti tra di loro. In formule: A'B' ≡ AB e A"B" ≡ AB implica A'B' ≡ A"B".
Da qui discendono (quasi) immediatamente le proprietà riflessiva, simmetrica e transitiva della congruenza.
ASSIOMA 3.3
Su una retta r sono dati due segmenti AB e BC che hanno il solo punto B in comune, e sulla stessa retta r o su un’altra retta r' sono dati due segmenti A'B', B'C' con il solo punto B' in comune. Allora se AB ≡ A'B' e BC ≡ B'C', anche AC ≡ A'C''.
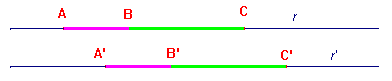Questo assioma
consente di definire la somma di segmenti, con la
proprietà che la somma di segmenti congruenti produca
segmenti congruenti (come naturalmente vogliamo che sia,
altrimenti che somma sarebbe?!).
ASSIOMA 3.4
Se 
ABC è un angolo e
B'C' una semiretta, allora esiste esattamente
una semiretta B'A' su ciascuno dei due lati
della retta B'C', tale che l'angolo
ABC e l'angolo A'B'C' siano congruenti. Inoltre
ogni angolo è congruente a se stesso.
In sostanza questo assioma afferma che in un piano si può costruire un dato angolo a partire da una data semiretta, su ciascuno dei due semipiani individuati dalla retta cui la semiretta appartiene.
ASSIOMA 3.5
Se per due triangoli \(ABC\) e \(A'B'C'\) si ha che
AB ≡ A'B', AC ≡ A'C' e
BAC ≡ B'A'C', allora anche ABC ≡ A'B'C'. Scambiando le notazioni si ha
anche che ACB
≡ A'C'B'.
Conseguenza fondamentale di questi assiomi, in particolare del 3.5 è il
Teorema 8
Se in due triangoli sono congruenti due lati e l'angolo compreso, allora i triangoli sono congruenti.
La dimostrazione di questo teorema (che esula dagli scopi di questa breve introduzione) è una conseguenza quasi immediata dell'assioma 3.5, tenendo anche conto dell'assioma 3.4. Si noti comunque che in questa impostazione assiomatica si arriva al famoso primo criterio di congruenza fra triangoli, dopo aver formulato ben 13 assiomi.
A questo punto si può cominciare a costruire una prima parte della geometria del triangolo, dimostrando gli altri due criteri di congruenza, e numerosi altri risultati di cui ci preme segnalare il famoso: in un triangolo un angolo esterno è maggiore degli angoli interni ad esso non adiacenti. Si tratta della famosa Proposizione 16 di Euclide, che, nella impostazione assiomatica di Hilbert non è più soggetta alle note critiche.