Parallelismo e continuità
Per concludere la presentazione degli assiomi posti da Hilbert a fondamento della geometria ci mancano il famoso assioma delle parallele (a tutti ben noto) e due ulteriori assiomi, poco conosciuti e poco citati invece nei testi di geometria piana.
ASSIOMA 4.1 - Assioma della parallele
Sia \(r\) una retta e \(A\) un punto fuori da essa. Esiste al più una retta nel piano individuato da \(r\) ed \(A\) che passi per \(A\) e non intersechi \(r\).
Si noti che l'assioma afferma solo l'unicità della parallela: l'esistenza di almeno una parallela è invece una conseguenza degli altri assiomi. Come già osservato nella pagina relativa alle geometrie non euclidee, la costruzione di una geometria in cui non esistono affatto parallele ad una retta data deve portare necessariamente anche alla modifica di qualche altro postulato della geometria.
L'introduzione dell'assioma delle parallele permette la costruzione di una geometria decisamente più semplice e "interessante". Una delle prime conseguenze di questo assioma è il fatto che la somma degli angoli interni di un triangolo è uguale a due angoli retti, risultato di cui si fa un uso continuo. Altra conseguenza di questo assioma (assieme naturalmente ai precedenti) è la possibilità di costruire un circolo per tre punti non allineati, ecc.
Non insistiamo oltre su questo assioma, sulla cui storia si potrebbe scrivere una intera enciclopedia. Segnaliamo solo che Hilbert afferma esplicitamente che dall'assunzione che non esistono parallele segue che la somma degli angoli di un triangolo è più grande di due retti. Inoltre ricorda anche che altri postulati oltre quello di parallelismo possono essere negati senza contraddizione, e che esistono molte altre geometrie logicamente possibili, oltre alle note geometrie non euclidee.
Passiamo ora a presentare gli ultimi due assiomi della geometria di Hilbert, detti anche Assiomi di continuità .
ASSIOMA 5.1 - Assioma di Archimede
Se \(AB\) e \(CD\) sono due segmenti qualsiasi, allora esiste un naturale /(n\) tale che \(n\) segmenti consecutivi \(CD\) costruiti a partire da \(A\) sulla semiretta da \(A\) verso \(B\) superano il punto \(B\).
ASSIOMA 5.2 - Assioma della completezza della retta
È impossibile ampliare i punti di una retta con il suo ordine e le sue relazioni di congruenza in modo da preservare le relazioni tra gli elementi originali e le fondamentali proprietà che derivano dall'ordine e dalla congruenza che discendono dagli assiomi del gruppo 1-3, e dall'assioma 5.1.
Il primo degli assiomi di continuità (Assioma di Archimede) era in realtà già adombrato da Euclide, nella Definizione quarta del Libro 5: Si dice che hanno fra loro rapporto grandezze le quali possono, se moltiplicate, superarsi reciprocamente.
Questo assioma è raramente introdotto in maniera esplicita nei testi elementari di geometria, probabilmente perché non è facile farne capire l'importanza. Come già per il postulato delle parallele, il suo significato si può capire a fondo solo costruendo un sistema dove esso non valga. Lo stesso Hilbert propone un modello di Geometria non archimedea, ma la sua trattazione non è semplice. Oggi l'idea di una retta reale non-archimedea ha assunto una grande importanza per l'uso che se ne fa nella costruzione dei numeri iperreali, introdotti, tra l'altro, per una trattazione alternativa del concetto di limite e di quelli connessi dell'analisi.
 Noi
vogliamo qui proporre un modello molto semplice in cui questo
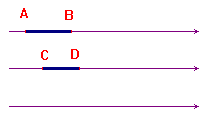
principio non vale, solo per aiutare a capire il problema. Si
consideri un insieme di due (o più) rette parallele, che
possiamo supporre equidistanti, tanto per fissare le idee. Su
ciascuna di esse si fissi lo stesso verso, per esempio da
sinistra a destra. I punti sulle rette si pensino disposti in
successione: quelli della prima retta vengono prima di quelli
della seconda, e così via. Per questo insieme di punti si
può anche parlare di segmenti congruenti, sia quando
stanno su una stessa retta, sia quando stanno su rette diverse,
e tuttavia esso è un insieme in cui non vale il principio
di Archimede: qualunque multiplo di un segmento che sta su una
retta non può mai superare un segmento che sta su una
retta successiva.
Noi
vogliamo qui proporre un modello molto semplice in cui questo
principio non vale, solo per aiutare a capire il problema. Si
consideri un insieme di due (o più) rette parallele, che
possiamo supporre equidistanti, tanto per fissare le idee. Su
ciascuna di esse si fissi lo stesso verso, per esempio da
sinistra a destra. I punti sulle rette si pensino disposti in
successione: quelli della prima retta vengono prima di quelli
della seconda, e così via. Per questo insieme di punti si
può anche parlare di segmenti congruenti, sia quando
stanno su una stessa retta, sia quando stanno su rette diverse,
e tuttavia esso è un insieme in cui non vale il principio
di Archimede: qualunque multiplo di un segmento che sta su una
retta non può mai superare un segmento che sta su una
retta successiva.
Per quanto riguarda l'assioma di continuità osserviamo che, a livello intuitivo, esso traduce in un assioma l'idea che "una retta non ha buchi", cioè è, appunto "un continuo", senza lacune. Questo fatto è di grande importanza quando si introduce il concetto di numero reale e si assume che la corrispondenza tra numeri reali e punti di una retta sia biunivoca.
Questo conclude la discussione sui fondamenti posti da Hilbert alla geometria. Per qualche ulteriore osservazione invitiamo a leggere la sezione Prima di lasciarci.