La proposizione 16 di Euclide
La proposizione 16 del Libro I degli Elementi di Euclide è molto interessante in quanto offre un facile spunto per una discussione sui fondamenti della geometria. Riportiamo l'enunciato e lo schema della dimostrazione originale.
Proposizione 16
In qualsiasi triangolo, se uno dei lati è prolungato, allora l'angolo esterno è più grande degli angoli interni ed opposti.
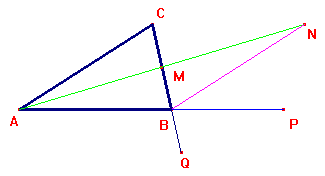 Sia ABC un triangolo e prolunghiamo il lato BC
in P. Considerato il punto medio M di
BC, congiungiamo A con M e lo
prolunghiamo in N, in modo che AM sia uguale
ad MN. I triangoli AMC ed NMB sono
uguali per avere uguali due lati e gli angoli di vertice
M. Ne segue che l'angolo ACB e
l'angolo CBN sono uguali. Poichè
CBN è una parte di CBP, si
deduce che l'angolo interno in C è minore
dell'angolo CBP. Bisecando AB si
può similmente provare che l'angolo interno
A è minore dell'angolo ABQ, che
è uguale all'angolo CMP. Questo consente di
concludere.
Sia ABC un triangolo e prolunghiamo il lato BC
in P. Considerato il punto medio M di
BC, congiungiamo A con M e lo
prolunghiamo in N, in modo che AM sia uguale
ad MN. I triangoli AMC ed NMB sono
uguali per avere uguali due lati e gli angoli di vertice
M. Ne segue che l'angolo ACB e
l'angolo CBN sono uguali. Poichè
CBN è una parte di CBP, si
deduce che l'angolo interno in C è minore
dell'angolo CBP. Bisecando AB si
può similmente provare che l'angolo interno
A è minore dell'angolo ABQ, che
è uguale all'angolo CMP. Questo consente di
concludere.
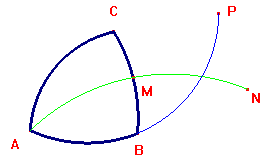 La dimostrazione sarebbe perfetta se si fosse sicuri che
CBN è una parte di CBP.
Purtroppo questo fatto non è una conseguenza degli
assiomi, né dei precedenti 15 teoremi già provati
negli Elementi. Euclide qui, come in altri posti, ha
implicitamente utilizzato l'evidenza della figura
per poter concludere.
La dimostrazione sarebbe perfetta se si fosse sicuri che
CBN è una parte di CBP.
Purtroppo questo fatto non è una conseguenza degli
assiomi, né dei precedenti 15 teoremi già provati
negli Elementi. Euclide qui, come in altri posti, ha
implicitamente utilizzato l'evidenza della figura
per poter concludere.
Purtroppo nulla ci autorizza a ritenere che la figura di sopra sia corretta, mentre quella qui a destra sia errata. L'unica evidenza possibile è costituita dal fatto che la prima figura sembra "più rispondente a quanto succede nel mondo reale", mentre la seconda ci appare artificiosa. E' ovvio che un tal modo di ragionare non può essere accettato in una teoria assiomatica, ma, in ogni caso, chi ci può garantire che la prima figura continuerebbe ad essere più "reale" anche a livello atomico o a livello delle dimensioni dell'universo?
E' chiaro che nel risolvere un problema di geometria la costruzione di una buona figura è fondamentale e può spesso fornire l'idea giusta, o aiutarci ad evitare di prendere cantonate, ma bisogna assolutamente tenere presente che una dimostrazione non può dipendere in maniera essenziale dalla figura. Proponiamo un ulteriore esempio per chiarire meglio il concetto.
Teorema: Ogni triangolo è isoscele.
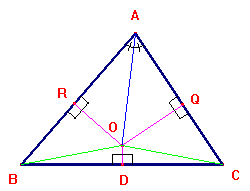 Per la dimostrazione si esamini la figura
qui a lato, dove ABC è un triangolo qualunque,
OD è l'asse del lato BC,
AO è la bisettrice dell'angolo BAC,
OR e OQ sono i segmenti di perpendicolare
condotti da O ai lati obliqui.
Per la dimostrazione si esamini la figura
qui a lato, dove ABC è un triangolo qualunque,
OD è l'asse del lato BC,
AO è la bisettrice dell'angolo BAC,
OR e OQ sono i segmenti di perpendicolare
condotti da O ai lati obliqui.
E' immediato che i triangoli ODB e ODC sono uguali, come pure i triangoli ARO e AOQ. Ne segue che sono uguali anche i triangoli BRO e OQC. Dunque AB=AR+RB è uguale ad AC=AQ+QC.
E' un utile esercizio (non troppo facile!) cercare di trovare l'errore basandosi unicamente sulla costruzione indicata, senza fare nuove figure. Se la cosa non vi riesce potete vedere la soluzione.
Bibliografia per questa pagina
- Maxwell E. A., Fallacies in Mathematics, Cambridge University Press, Cambridge, 1959
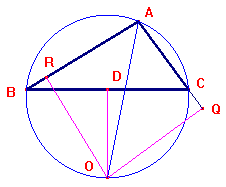 L'errore sta nell'aver disegnato
il punto O interno al triangolo. Infatti l'asse
del segmento BC e la bisettrice dell'angolo
BAC devono, se non coincidono, necessariamente
incontrarsi nel punto medio dell'arco BC di
circonferenza circoscritta, cioè all'esterno del
triangolo. Una costruzione accurata della figura renderebbe
subito evidente l'errore.
L'errore sta nell'aver disegnato
il punto O interno al triangolo. Infatti l'asse
del segmento BC e la bisettrice dell'angolo
BAC devono, se non coincidono, necessariamente
incontrarsi nel punto medio dell'arco BC di
circonferenza circoscritta, cioè all'esterno del
triangolo. Una costruzione accurata della figura renderebbe
subito evidente l'errore.