Indagini sulla continuità - 2
Consideriamo la funzio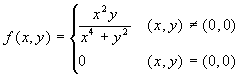ne 
. Il suo grafico
è rappresentato nella figura qui sotto a sinistra, mentre
nella figura a destra sono anche rappresentate alcune curve di
livello. Il grafico è necessariamente molto approssimato
nei pressi dell'origine.
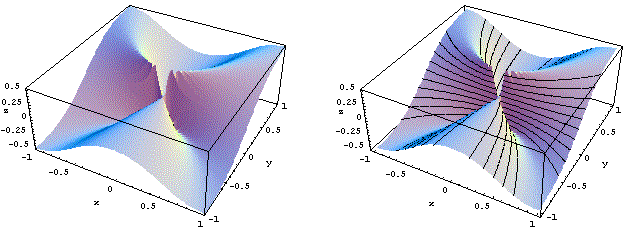
E' interessante considerare le sezioni di questa superficie con piani verticali contenenti l'asse z, cioè considerare la restrizione della funzione alle rette passanti per l'origine. Nelle figure qui sotto abbiamo rappresentato le curve ottenute dall'intersezione della superficie con i piani x - y = 0 e x + y = 0, sia tracciandole sulla superficie che nel piano sezione.
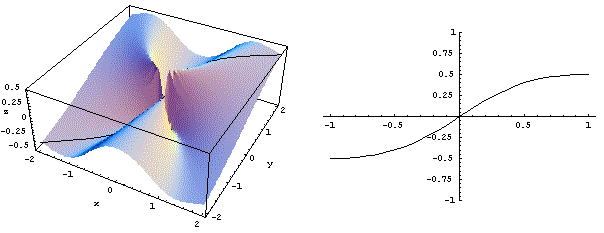
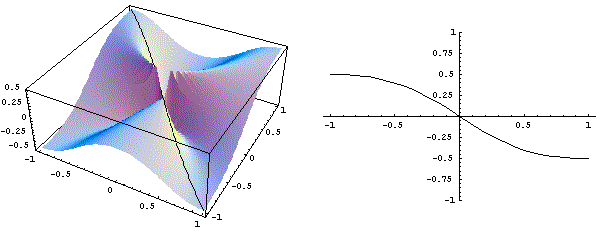
E' interessante notare come tutte queste curve siano curve continue (addirittura derivabili) anche nell'origine. Discorso analogo vale per qualunque altra sezione con un piano verticale contenente l'asse z: la restrizione della funzione ad una retta per l'origine è sempre una curva continua, in particolare la restrizione agli assi coordinati coincide con gli assi stessi. Purtroppo questo non è sufficiente a garantire la continuità. Se infatti proviamo a fare la restrizione della funzione alle parabole y = ±x2, otteniamo due curve sulla superficie che si trovano a quota costante (±0.5): ciò significa che in un intorno dell'origine ci sono punti dove la funzione è "distante" da zero, e quindi non potrà avere limite zero, ovvero non potrà essere continua. Si veda il grafico qui sotto.
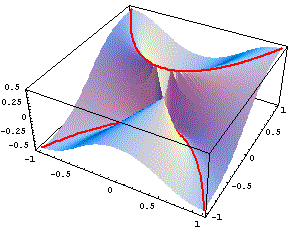
Quanto succede con questa superficie è molto interessante ed è sempre collegato al fatto che, in R2, ci sono infiniti modi per tendere ad un punto, a partire da un altro punto situato in un intorno.