Introduzione intuitiva ai limiti e alla continuità per funzioni di due variabili

Scopo di queste pagine è di visualizzare, utilizzando esclusivamente considerazioni grafiche, alcune caratteristiche delle funzioni di due variabili, con particolare riguardo alle questioni legate al calcolo dei limiti e alla continuità. Naturalmente le idee qui esposte non sono sostitutive della teoria generale, e sono pensate solo per facilitare la comprensione dei problemi connessi all'estensione a più dimensioni delle tecniche dell'analisi.

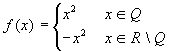Il grafico di una funzione di due variabili (f: AR² → R) è, in senso lato, una superficie di R³. Come è ben noto, nel caso delle funzioni di una variabile reale il grafico é una curva, ma naturalmente può trattarsi di una curva molto "strana". Si pensi, per esempio, alla funzione , il cui grafico è rappresentato qui sotto, ma solo in modo molto poco "realistico". Si tratta di una funzione che è discontinua dappertutto tranne che nell'origine, dove è addirittura derivabile, con derivata uguale a zero. Dunque, mentre fuori dall'origine il grafico è costituito da punti che "saltano continuamente" dalla parabola y = x², alla y = -x², nell'origine esso ammette addirittura retta tangente!

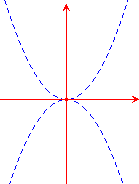
Le cose possono essere molto più complicate per le funzioni di due variabili e questo è legato, per quanto riguarda le questioni connesse al concetto di limite, al fatto che, mentre in una variabile gli intorni dei punti sono, nella sostanza, segmenti, nel piano essi sono dischi: ciò significa che esiste essenzialmente un solo modo di "tendere ad un dato punto" in R, mentre esistono infiniti modi in R².

Per rendersi conto a livello intuitivo di come vanno le cose per le funzioni di due variabili si possono usare varie tecniche e non sempre il grafico (comunque di solito molto difficile da rappresentare!) può essere sufficiente. I programmi di computer grafica, come Derive™, Maple™, Mathematica™ o simili, sono di grande aiuto, ma è opportuno avere le idee precise su alcune situazioni ricorrenti, per evitare di compiere errori grossolani. Le pagine che seguono trattano in dettaglio questo problema.