La polvere di Cantor
Consideriamo l'intervallo [0,1] dei reali, intervallo che
indicheremo con C0. Lo dividiamo in tre
parti uguali mediante i punti 1/3 e 2/3. Se gettiamo via la
parte centrale, senza gli estremi, rimaniamo con l'insieme
C1= [0,1/3]![]() [2/3,1].
Se ripetiamo il procedimento su ciascuna delle due parti di cui
è costituito C1, otteniamo
l'insieme C2=[0,1/9]
[2/3,1].
Se ripetiamo il procedimento su ciascuna delle due parti di cui
è costituito C1, otteniamo
l'insieme C2=[0,1/9]![]() [2/9,1/3]
[2/9,1/3]![]() [2/3,7/9]
[2/3,7/9]![]() [8/9,1].
Ripetiamo il procedimento all'infinito, senza mai stancarci,
ottenendo gli insiemi C3,
C4, ...,Cn,...
[8/9,1].
Ripetiamo il procedimento all'infinito, senza mai stancarci,
ottenendo gli insiemi C3,
C4, ...,Cn,...
L'insieme di Cantor, o Polvere di Cantor, è
l'insieme: ![]() .
.
Una rappresentazione grafica, necessariamente limitata ai primi passi, di questo procedimento può essere la seguente:
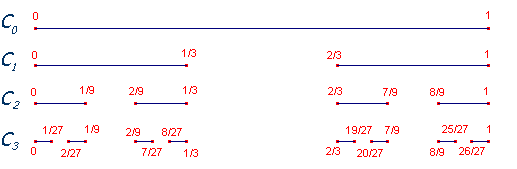
Si noti che, per ogni n, le due metà di Cn+1, sono una copia esatta, ridotta di 1/3, di Cn. Questo significa che guardare Cn+1 con una lente che ingrandisca tre volte è lo stesso che guardare Cn ad occhio nudo. Si osservi altresì che la figura sopra riportata non è una rappresentazione dell'insieme di Cantor, ma solo del procedimento utilizzato per ottenerlo: non c'è alcuna possibilità di ottenere una qualche rappresentazione corretta dell'insieme che stiamo considerando.
L'insieme di Cantor gode di una serie di straordinarie proprietà, e viene spessissimo utilizzato per costruire esempi di notevole interesse in matematica. Tra questi citiamo una particolare funzione reale di variabile reale, detta scala diabolica o funzione di Vitali, di cui proponiamo la trattazione.
Le prime proprietà che ci interessano sono il fatto che ha "lunghezza" nulla. e che ha la stessa cardinalità di R. Dal punto di vista topologico occorre aggiungere che l'insieme C, come sottoinsieme di R, è compatto, ovunque non denso, totalmente sconnesso, perfetto. Anche se la comprensione precisa di queste ultime caratteristiche richiede almeno un minimo di conoscenze di topologia, la sostanza si può intuire abbastanza facilmente: l'insieme in questione ha tanti punti quanti lo stesso insieme di partenza, pur avendo lunghezza nulla; inoltre non contiene alcun intervallo, nemmeno "piccolissimo", mentre "nei pressi di ogni suo punto" esiste sempre almeno un segmento, opportunamente piccolo, che non sta nell'insieme.
![]() Per quanto riguarda il fatto che la
curva ha lunghezza nulla è da segnalare che, se è
vero che un po' alla volta il segmento viene
"svuotato" del suo contenuto, è anche vero che,
ad ogni passo, si toglie solo 1/3 della lunghezza, lasciandone
dunque i 2/3, cioè la maggior parte. Indipendentemente
dal livello raggiunto, ciò che resta è più
di ciò che viene prelevato, ed è allora ben strano
che alla fine resti una lunghezza nulla. Dunque la lunghezza
è zero o no? Il calcolo matematico mostra di si, ma
l'intuizione suggerisce che sarebbe meglio approfondire il
problema.
Per quanto riguarda il fatto che la
curva ha lunghezza nulla è da segnalare che, se è
vero che un po' alla volta il segmento viene
"svuotato" del suo contenuto, è anche vero che,
ad ogni passo, si toglie solo 1/3 della lunghezza, lasciandone
dunque i 2/3, cioè la maggior parte. Indipendentemente
dal livello raggiunto, ciò che resta è più
di ciò che viene prelevato, ed è allora ben strano
che alla fine resti una lunghezza nulla. Dunque la lunghezza
è zero o no? Il calcolo matematico mostra di si, ma
l'intuizione suggerisce che sarebbe meglio approfondire il
problema.
Per come è stato costruito verrebbe da pensare che alla fine, dopo aver eliminato tutto quello che c'era da eliminare, in C siano rimasti solo gli estremi degli intervalli che sono stati eliminati: ci si rende conto invece subito che non può essere così, perché gli intervalli eliminati, e quindi anche i loro estremi, sono in quantità numerabile, mentre C non è numerabile. Un punto diverso dagli estremi, e che sta in C, è 1/4: la sua rappresentazione in base 3 è infatti data dal numero 0,020202..., cioè è un numero contenente solo le cifre 0 e 2, dunque sta in C. Per convincersene basta osservare che (4)10=(11)3 ed eseguire la divisione tra 1 e (11)3 (per capire meglio il calcolo si ricordi che la successione di numeri, in base 3, a partire da 1, si può scrivere così: 1, 2, 10, 11, 12, 20, 21, 22, 100, ecc.):
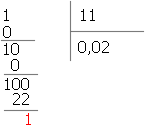
Che 1/4 non coincida poi con nessuno degli estremi dei segmenti soppressi risulta evidente per il fatto che il suo denominatore non è una potenza di 3.
Un'altra caratteristica interessante di C è il fatto che esso contiene infinite copie di se stesso, in scala ridotta: basta ricordare che già Cn, come abbiamo più sopra osservato, contiene due copie, in scala ridotta di 1/3, di Cn-1. Questo fatto implica che l'ingrandimento di una qualunque porzione di C è sempre simile a C, ovvero che, anche se si esamina una porzione infinitamente piccola di C, la complessità di C non diminuisce. E' proprio questa caratteristica che rende C un frattale.