Solo per i raffinati
Come dice il titolo, questa pagina è inserita solo per i più raffinati e lo scopo è quello di mostrare che, anche con funzioni monotòne, l'asintoto non può, in generale, essere considerato come la "tangente all'infinito" al grafico di una funzione.
Cominciamo col considerare la funzione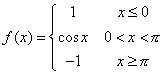 
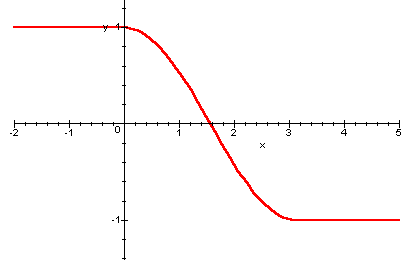
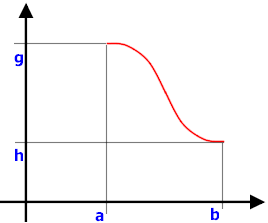
Si verifica subito che essa è derivabile per ogni x. Con un significativo linguaggio geometrico si può affermare che la funzione cosx realizza un "ponte" tra (0,1) e (π,-1), in modo da ottenere una funzione derivabile. Si possono costruire ponti tra due punti qualunque (a,g) e (b,h) operando una traslazione di assi con cambiamento di scala, cioè un'affinità, del tipo
.
Se si tiene conto che (0,1) deve corrispondere a (a,g) e (π,-1) a (b,h), si trova facilmente che l'affinità ha le equazioni seguenti:
.
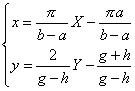Sostituendo in y=cosx, si ottiene la funzione e il grafico che segue:
La derivata di questa funzione nel punto medio,
xM, del segmento [a,b] vale 
.
Possiamo ora considerare la funzione seguente (è più facile da disegnare che da scrivere!):
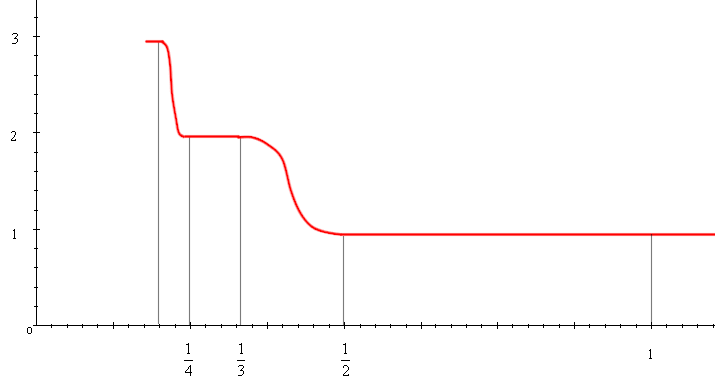
E' immediato che questa funzione ha l'asse delle y come asintoto verticale e che è decrescente. La sua derivata vale zero in tutti i tratti orizzontali, mentre tende a -∞ nel centro degli altri tratti (è sufficiente ricordare l'espressione trovata prima e osservare che, in questo caso, g-h vale sempre 1, mentre b-a tende a zero): ciò basta per dire che la derivata della funzione non può avere limite se x tende a zero, cioè che l'asintoto non è "tangente all'infinito". Questo fatto risulta evidente dal grafico: i tratti "ponte" diventano sempre più verticali, mentre gli altri tratti rimangono sempre "orizzontali".
Si può costruire un esempio simile per l'asintoto orizzontale. Basta, per esempio, considerare una funzione "ponte" che abbia derivata infinita al centro dell'intervallo [a,b] e dimensionarla opportunamente come fatto sopra. Si può poi considerare la funzione:
.
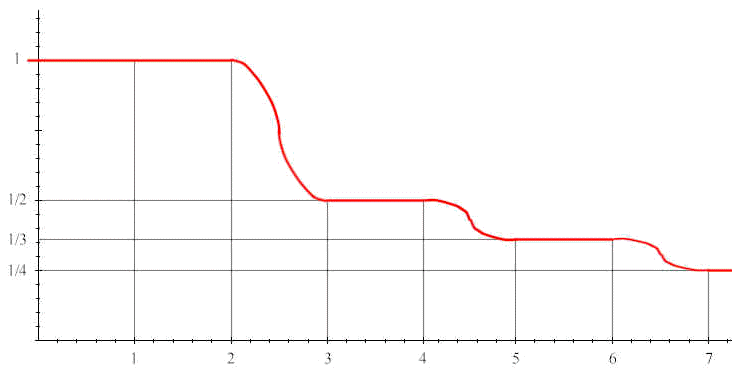
Questa funzione, in ogni intorno di +∞, ha punti con derivata nulla e punti con derivata infinita, dunque la derivata non tende ad alcun limite: neanche in questo caso l'asintoto è la "tangente all'infinito".
Ci preoccuperemo ora di ricercare una condizione sufficiente
affinché l'asintoto sia effettivamente la
"tangente all'infinito". Sia f(x)
una funzione definita in un intervallo avente come estremo
destro il numero reale b. Si supponga che f
abbia in questo intervallo (escluso eventualmente b), derivata
prima e seconda, cha la derivata seconda sia sempre positiva, e
che 
. In queste
ipotesi si può provare che
anche la derivata prima ha per limite +∞, cioè che
la tangente al grafico, quando x tende a c da sinistra, tende a
coincidere con l'asintoto. La tesi di questo teorema
è abbastanza intuitiva, in quanto in questo caso la
funzione ha la concavità sempre "dalla stessa
parte". In modo analogo si può considerare una
funzione definita in un intervallo superiormente illimitato e
ivi dotata di derivate prima e seconda, con derivata seconda
positiva, e avente limite finito, k, per x tendente
all'infinito. In queste ipotesi si può provare che la
derivata prima ha per limite lo zero, cioè che la
tangente al grafico tende a coincidere con l'asintoto
(tangente orizzontale e quindi derivata nulla). In modo analogo
si può concludere in tutti gli altri casi.
Si può allora concludere che
Condizione sufficiente affinché l'asintoto coincida con la "tangente all'infinito" è che la funzione sia convessa, oppure concava, in un opportuno intorno dell'infinito per gli asintoti orizzontali ed obliqui, di un punto c per gli asintoti verticali.
Si noti come la funzione 
fornisca un esempio che prova che la
condizione non è, in generale, necessaria: si tratta
infatti di una funzione che non è né concava
né convessa in un intorno di +∞, ma che ha per
tangente all'infinito proprio l'asintoto orizzontale.
