Asintoti e tangenza all'infinito
L'asintoto, verticale, orizzontale od obliquo, è spesso considerato come la "tangente all'infinito" al grafico di una funzione. Vogliamo far vedere su alcuni esempi come questa affermazione non abbia alcuna giustificazione, per lo meno con la definizione di asintoto che abbiamo dato noi.
Il problema che ci poniamo é il seguente: se la funzione si avvicina all'asintoto, che ne é della tangente alla funzione? E' da ritenere che essa tenda a coincidere con l'asintoto?
Analizziamo per esempio il caso dell'asintoto obliquo. Per
la sua ricerca occorre calcolare il limite di 
, dopo aver verificato che la funzione tende
all'infinito. Supponiamo che la funzione sia derivabile.
Poiché questo limite si presenta nella forma
indeterminata 
si può applicare la
regola di l’Hôpital: dato che il limite del
denominatore vale 1, ci resta da calcolare il limite di
f'(x). Possiamo dunque concludere che
se il limite di f’(x) esiste
finito e diverso da zero, allora esso coincide
con il coefficiente angolare dell'eventuale
asintoto (occorrerà ancora calcolare il limite di
f(x)–mx, per vedere se l’asintoto
c’è oppure no); se però il limite della
derivata prima non esiste non possiamo affermare che
l'asintoto non c’è, in quanto il limite di potrebbe ugualmente esistere. Se l'asintoto
c’è, nonostante la derivata prima non abbia limite,
allora sicuramente la tangente alla funzione
non tende a coincidere con l'asintoto. Una
considerazione simile vale anche per gli asintoti verticali.
In quel che segue faremo esempi relativi ad asintoti verticali ed orizzontali. Si osservi però che da essi si possono ottenere immediatamente esempi relativi ad asintoti obliqui. Se infatti una funzione f(x) ha per asintoto orizzontale, a +∞, la retta y=k, allora la funzione g(x)=f(x)-k+mx+q ha per asintoto obliquo la retta y=mx+q. La dimostrazione è un semplice esercizio e il risultato è intuitivamente ovvio.
Esempio 1
Si consideri la funzione 
. Si vede subito che y=0 è un asintoto
orizzontale. Essendo 
, se ne deduce che
f'(x) non ha limite, e quindi la tangente al
grafico della funzione non tende ad un'inclinazione
determinata quando x si allontana all'infinito. Si osservi
che questa funzione oscilla tra 
e 
, tagliando infinite volte
l'asintoto.
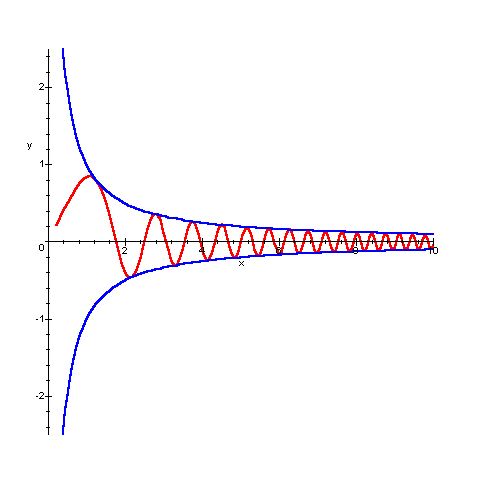
Non si creda però che quando una funzione è
oscillante e "passa continuamente da sopra a sotto
l'asintoto", allora la sua tangente non tende ad una
posizione determinata. Si consideri a questo proposito la
funzione 
. La retta y=0 è ancora un asintoto
orizzontale, ma ora anche f'(x) tende a zero, come
mostra un calcolo immediato, cioè la funzione e
l'asintoto tendono ad essere tangenti
all'infinito.
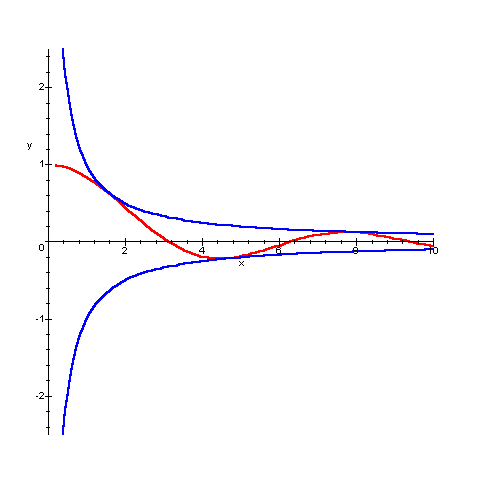
É interessante esaminare il motivo di questo diverso
comportamento, per funzioni che compiono infinite oscillazioni,
apparentemente dello stesso tipo, in un intorno di +∞.
Cercheremo di dare una spiegazione intuitiva, anche se poco
"rigorosa". Si noti che la funzione sinx
oscilla tra -1 ed 1, e lo spazio richiesto per una oscillazione
completa è costantemente uguale a 2π. Anche la
funzione sin(x2) oscilla tra -1 ed 1, ma ora
lo spazio richiesto per un'oscillazione completa diventa sempre più piccolo, man mano
che x cresce. Moltiplicare una funzione come questa per 
significa "schiacciare le oscillazioni".
É ovvio che se le oscillazioni avvengono in uno spazio
grande, questo "schiacciamento" avrà effetto
anche sulla tangente, mentre se le oscillazioni avvengono in uno
spazio piccolo, anzi via via più piccolo man mano che x
cresce, l'influenza sulla tangente sarà molto meno
importante.
Esempio 2
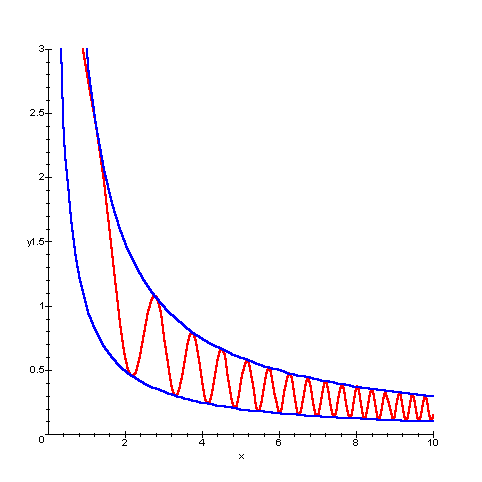
Si consideri la funzione 
, con
x>0, il cui grafico, compreso tra le curve 
e 
, è rappresentato
qui sotto.
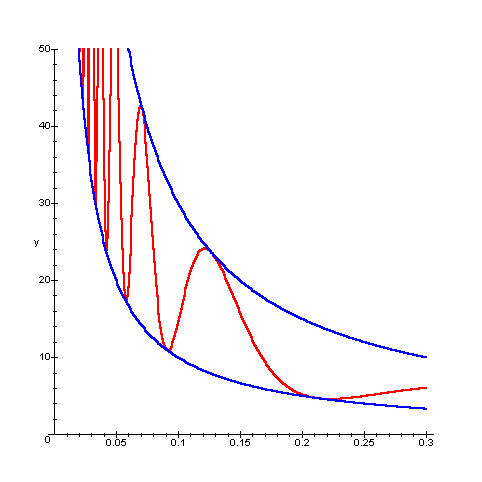
Un calcolo immediato, o la semplice osservazione che il grafico
è compreso tra le due curve e , prova che x=0
è asintoto verticale per la curva. Si ha poi 
. Se calcoliamo questa derivata nei punti 
, punti che si avvicinano a zero al crescere
di k, si ottiene
f'(x)=-(2kπ)2(2kπ+2). Su questi
punti la derivata tende dunque a -∞. Se ripetiamo il
calcolo sui punti 
, troviamo che la
derivata tende, invece, a +∞. Considerata la
continuità della derivata stessa se ne deduce che essa si
annulla in infiniti punti, in ogni intorno destro dello zero.
Questo basta per affermare che la derivata non può avere
un limite quando x tende a zero, e cioè che la funzione
non tende a diventare tangente al suo asintoto.
Esempio 3
Si consideri ora la funzione 
. E' immediato che 
, cioè che il grafico della funzione è
esterno a quello di e di . Inoltre il limite, per 
, vale ∞, (non +∞, né -∞),
cioè la funzione ha l'asse delle ordinate come
asintoto verticale. La funzione ha, inoltre, infiniti asintoti
verticali, di equazione 
, in ogni intorno
destro dell'origine. E' evidente che per una funzione
come questa non ha alcun senso pensare all'asse delle
ordinate, che è asintoto verticale, come
"tangente all'infinito".
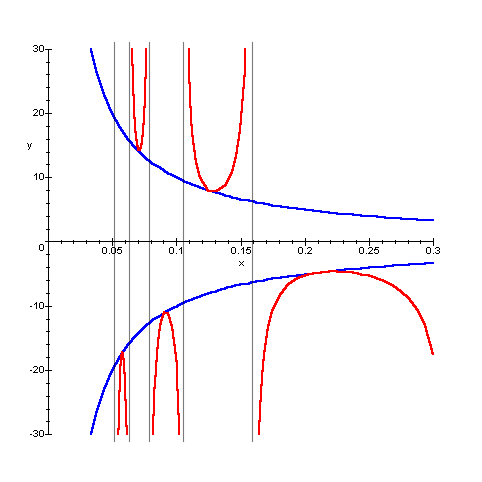
Esempio 4
Si consideri la funzione 
. E' immediato che la funzione è compresa tra
le due curve e , e che y=0 è un asintoto orizzontale.
Questa funzione però, a differenza di quelle
dell'esempio 1, sta sempre sopra l'asintoto. Anche qui
però un facile calcolo mostra che la derivata prima non
ha limite, cioè che la tangente non assume una posizione
determinata, quando x cresce all'infinito.
Questi esempi provano come il concetto di asintoto che abbiamo introdotto non abbia, in generale, nulla a che fare con quello di inclinazione limite per la tangente.
Considerata la natura degli esempi proposti si potrebbe pensare che tali "anomalie" siano proprie delle funzioni oscillanti. In realtà si possono portare anche esempi di funzioni monotòne con le stesse caratteristiche.