Limiti - Uso degli ordini di infinito e infinitesimo
Riportiamo qui solo le nozioni essenziali utili per il calcolo dei limiti, senza alcuna pretesa di completezza, e in maniera completamente informale. Segnaliamo che la nomenclatura qui introdotta non è universalmente adottata, e potrebbe essere notevolmente "razionalizzata".
Supporremo che le funzioni di cui ci occupiamo siano diverse da zero in un intorno di un punto c, escluso eventualmente c.
Definizioni fondamentali
-
Una funzione si dice infinitesima, per x
tendente a c, se
-
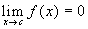
Una funzione si dice infinita, per x
tendente a c, se
.
-
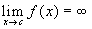Date due funzioni f e g, entrambe
infinitesime per x tendente a c, si dice
che:
-
f è infinitesimo di ordine superiore a
g se
-
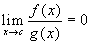
f è infinitesimo di ordine inferiore a
g se
-
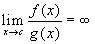
f è infinitesimo dello stesso ordine di
g se
-
f è infinitesimo di ordine superiore a
g se
-
Date due funzioni f e g, entrambe infinite
per x tendente a c, si dice che:
-
f è infinito di ordine superiore a
g se
-
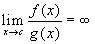
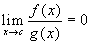
f è infinito di ordine inferiore a
g se
-
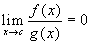
f è infinito dello stesso ordine di
g se
-
f è infinito di ordine superiore a
g se
Principio di sostituzione
L'applicazione dei concetti sopra introdotti al calcolo dei limiti si basa sul cosiddetto principio di sostituzione, di cui enunciamo qui una forma semplificata.
-
Caso degli infinitesimi. Se f,
f1, g e g1
sono funzioni infinitesime per x tendente a
c, e se f1 e
g1 sono di ordine superiore a f
e g, allora se esiste il
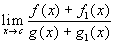, esiste anche, con lo stesso valore, il 
.
-
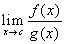Caso degli infiniti. Se f,
f1, g e g1
sono funzioni infinite per x tendente a c,
e se f1 e g1
sono di ordine inferiore a f e g, allora se
esiste il 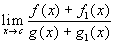, esiste anche,
con lo stesso valore, il .
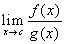In sostanza il teorema afferma che, nel calcolo del limite di un rapporto di infinitesimi o di infiniti si possono trascurare gli infinitesimi di ordine superiore e gli infiniti di ordine inferiore. Si tratta di un teorema che, se ben applicato, consente notevoli semplificazioni nel calcolo dei limiti.
Ordini rispetto ad un campione
- Date due funzioni f e g, entrambe infinitesime o entrambe infinite per x tendente a c, si dice che f ha ordine (di infinitesimo o di infinito) α (>0), rispetto a g, se f e |g|α hanno lo stesso ordine. Si usa dire che f ha ordine α rispetto all'infinitesimo campione g.
-
Nel caso di x tendente a c
R si assume come campione standard
di infinitesimi la funzione g(x) =
x-c, come campione standard di infiniti la
funzione g(x) = 1/(x-c).
- Nel caso di x tendente a ∞ si assume come campione standard di infinitesimi la funzione g(x) = 1/x, come campione standard di infiniti la funzione g(x) = x.
- Quando si parla di "ordine di infinito" si intende sempre ordine rispetto al campione standard.
- Purtroppo, in generale, una funzione infinita o infinitesima non ha un ordine rispetto al campione standard. Si usano spesso, in questi casi, nomenclature come "ordine soprareale, infrareale, sottoreale". Questi concetti non hanno però una grande importanza nel problema del calcolo dei limiti. La cosa essenziale da ricordare è il principio di sostituzione sopra menzionato, dove non conta l'ordine, ma l'essere di "ordine superiore" o di "ordine inferiore".
Alcuni casi importanti (conseguenze di limiti notevoli)
- Per x tendente a +∞ lnx ha ordine (di infinito) inferiore a qualunque potenza di x.
- Per x tendente a +∞ ex ha ordine (di infinito) superiore a qualunque potenza di x.
- Per x tendente a +∞ coshx, sinhx ed ex hanno lo stesso ordine (di infinito).
- Per x tendente a zero, sinx, ln(1+x), ex-1, tanx hanno ordine 1, 1-cosx ha ordine 2.
Il simbolo "o piccolo"
Il simbolo o piccolo, introdotto da Edmund Landau (nel
1909) è molto usato nella teoria degli infiniti ed
infinitesimi. Si dà la seguente definizione: f è o
piccolo di g, per x → c, se
.
In sostanza dire che f è o piccolo di g, significa dire che f è "infinitamente più piccola" di g, ovvero che è, se infinitesimo, di ordine superiore, se infinito, di ordine inferiore. Con questa notazione il principio di sostituzione si può enunciare semplicemente dicendo che si possono "trascurare gli o piccolo", in un calcolo di limiti coinvolgenti infiniti o infinitesimi.
Algebra degli infiniti ed infinitesimi
- La somma di due infinitesimi di ordine α e β con α<β è un infinitesimo di ordine α.
- La somma di due infiniti di ordine α e β con α<β è un infinito di ordine β.
- La somma di due infinitesimi di ordine α è un infinitesimo di ordine ≥α.
- La somma di due infiniti di ordine α o non è un infinito, o è un infinito di ordine ≤α.
- Il prodotto di due infinitesimi (o infiniti) di ordine α e β è un infinitesimo (o infinito) di ordine α+β.