Problemi di massimo e minimo - Suggerimenti per la soluzione
1.11 Sia k>0 un numero reale. Si trovi il
minimo assoluto di 
.
Si può osservare che la funzione data rappresenta la somma delle distanze di un generico punto del piano dai punti (0,k) e (k,0). Il valore minimo è a√(2).
1.12 Data la funzione f(x,y) = x2+xy+y2+2x+3 y, ricercarne gli estremi relativi, senza l'uso delle derivate seconde.
Il solo punto critico è (-1/3, -4/3). Per deciderne la
natura senza l'uso delle derivate seconde occorre valutare i
valori di f in un intorno del punto, rispetto al valore
nel punto. Conviene eseguire la traslazion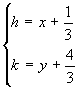e 
, che trasporta il punto critico nell'origine. Si
ottiene g(h,k) =
h2+hk+k2-7/3.
Allora g(h,k)-g(0,0) =
h2+hk+k2.
Quest'ultima quantità è sempre positiva, per
cui il punto in questione è un minimo. (Se h e k sono
concordi è ovvio che
h2+hk+k2
è positivo; se sono discordi basta osservare che
h2+hk+k2 =
(h+k)2-hk, che è
una somma di quantità positive).
1.15 Detti x,y,z i lati del triangolo, il vincolo si può scrivere x+y+z=2p, con x≥0, y≥0, z≥0. Si tratta di un insieme compatto, costituito dalla parte di piano x+y+z=2p contenuta nel primo ottante. Qui sotto è rappresentato questo vincolo per il caso particolare p=1. La formula che permette il calcolo dell'area a partire dai lati è quella di Erone: A2=p(p-x)(p-y)( p-z) (ci si può limitare a calcolare il massimo di A2 perché la radice è una funzione crescente).
La funzione Lagrangiana è dunque L(x,y,z,λ)=p(p-x)( p-y)(p-z)+λ(x+y+z-2p). Il punto critico è x=y=z=2p/3. Poichè la funzione ha necessariamente minimo sui bordi del vincolo (quando almeno uno dei tre lati è zero), si conclude subito che il punto critico trovato è il massimo, che corrisponde al triangolo equilatero.