Problemi di massimo e minimo - Soluzione 1.7
Calcolare i punti di massimo o minimo per la funzione f(x,y) = x4+y4-2(x2+ y2)+4xy.
La funzione è elementare con dominio R2, pertanto non presenta problemi di regolarità.
Il gradiente e la matrice Hessiana sono dati da: 
f(x,y) =
(4x3-4x+4y,
4y3-4y+4x) 
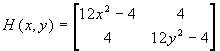. I punti critici si trovano facilmente e sono (0,0),
dove l'Hessiano è nullo, (√(2),-√(2)) e
(-√(2),√(2)). Con un calcolo standard si prova che
questi due ultimi punti sono di minimo e il minimo vale -8. Per
decidere la natura del primo punto critico occorre
un'analisi della funzione in un opportuno intorno.
Poiché f(0,0) = 0, si tratta di valutare il
segno della funzione. Si può osservare che sui punti
della retta y=x la funzione vale
2x4, per cui è positiva, mentre sui
punti dell'asse x vale
x2(x2-2), e quindi
assume valori negativi (almeno nei pressi di zero). Ciò
basta per concludere che il punto in questione non è
né di massimo né di minimo.
Le due figure qui sotto mostrano la superficie con alcune curve di livello (a sinistra) e la stessa superficie con le due curve che abbiamo usato per valutare la natura del punto (0,0).
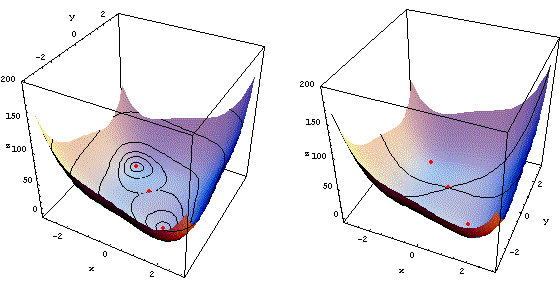
Nelle due figure qui sotto abbiamo tracciato le curve 2x4 e x2(x2-2) per una migliore visualizzazione del segno della funzione.
