Problemi di massimo e minimo - Soluzione 1.3
Calcolare i punti di massimo, minimo o sella per la funzione f(x,y) = x4+x2y+y 2+3.
La funzione è elementare con dominio R2, pertanto non presenta problemi di regolarità.
Il gradiente e la matrice Hessiana sono dati da: ![]() f(x,y) =
(4x3+2xy,x2+2
y) e
f(x,y) =
(4x3+2xy,x2+2
y) e 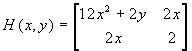 . Il gradiente si annulla solo in
(0,0), dove l'Hessiano è nullo. Dobbiamo quindi
decidere con uno studio locale la natura del punto critico
trovato. L'idea è quella di cercare di scrivere la
funzione in modo tale che sia facile valutare i suoi valori
rispetto al valore f(0,0) = 3. Per questo
osserviamo che i primi tre addendi, con una semplice
modifica, possono essere pensati come lo sviluppo di un
quadrato. Si ottiene:
. Il gradiente si annulla solo in
(0,0), dove l'Hessiano è nullo. Dobbiamo quindi
decidere con uno studio locale la natura del punto critico
trovato. L'idea è quella di cercare di scrivere la
funzione in modo tale che sia facile valutare i suoi valori
rispetto al valore f(0,0) = 3. Per questo
osserviamo che i primi tre addendi, con una semplice
modifica, possono essere pensati come lo sviluppo di un
quadrato. Si ottiene: 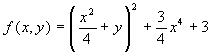 . Questo ci permette
di concludere che la funzione assume sempre valori superiori a
3, ovvero che (0,0) è un punto di minimo relativo (e anzi
assoluto). La funzione non può avere massimi assoluti
perché, per esempio, sulla retta x = 0 tende
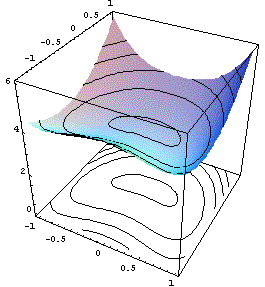
all'infinito se y tende all'infinito. Si veda
il grafico qui sotto, dove abbiamo anche tracciato alcune curve
di livello per evidenziare l'andamento del grafico.
. Questo ci permette
di concludere che la funzione assume sempre valori superiori a
3, ovvero che (0,0) è un punto di minimo relativo (e anzi
assoluto). La funzione non può avere massimi assoluti
perché, per esempio, sulla retta x = 0 tende
all'infinito se y tende all'infinito. Si veda
il grafico qui sotto, dove abbiamo anche tracciato alcune curve
di livello per evidenziare l'andamento del grafico.