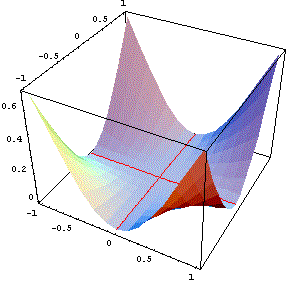Problemi di massimo e minimo - Soluzione 1.1
Calcolare i punti di massimo, minimo o sella per la funzione f(x,y) = ln(1+x2y2).
Si tratta di una funzione elementare, con dominio R2 e che non presenta problema di regolarità. Poiché la funzione logaritmo è strettamente crescente ci si può limitare a studiare la funzione g(x,y) = 1+x2y2 (non ci sarebbe comunque alcuna difficoltà suppletiva se studiassimo direttamente la funzione data).
Il gradiente di g è dato da 
g(x,y) =
(2xy2,2x2y).
Esso si annulla su tutti i punti dei due assi coordinati,
cioè (x,0) e (0,y). La matrice Hessiana
è: 
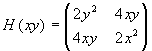. Purtroppo la
matrice risulta nulla nell'origine e solo semidefinita sugli
altri punti critici trovati: dall'esame delle derivate
seconde non posso concludere nulla circa il carattere dei punti
stazionari. Si ha però
1+x2y2 ≥1 e la
funzione g vale esattamente 1 sui punti critici
trovati. Essi saranno pertanto punti di minimo assoluto
(oltrechè relativo, ovviamente).
Il grafico qui sotto rende evidente il risultato trovato. Abbiamo anche tracciato le due rette che si ottengono sezionando la superficie con i piani coordinati, per visualizzare il fatto che le derivate parziali sono nulle lungo i due assi.
