Problemi di massimo e minimo - Soluzione 1.14
Trovare il massimo e minimo assoluto della funzione f(x,y,z) = x, con le condizioni x2+y2+z2=5/2 e y+z=1.
Intanto osserviamo che il vincolo è l'intersezione
tra una sfera e un piano, per cui è un cerchio, regione
chiusa e limitata: il massimo e il minimo esistono sicuramente.
Poi controlliamo il rango della matrice costruite con le
derivate dei vincoli. Si ha: 
, che ha rango 1
solo nei punti (0,t,t), che non appartengono al
vincolo. Derivando la funzione Lagrangiana si ha il sistema:
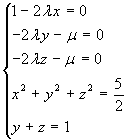, che ha solo le soluzioni 
. Per sostituzione diretta si trova che il primo punto
è di massimo, il secondo di minimo.