Problemi di massimo e minimo - Soluzione 1.13
Calcolare i punti di massimo e minimo relativo per la funzione f(x,y) = x2y3(6-2x-3y).
Cominciamo a calcolare il gradiente e l'Hessiano della
funzione. Si ha ![]() f(x,y) =
(12xy3-6x2y
3-6xy4,18x2y
2-6x3y2-12x
2y3),
f(x,y) =
(12xy3-6x2y
3-6xy4,18x2y
2-6x3y2-12x
2y3), 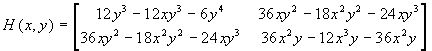 . Si trovano
facilmente i seguenti punti critici (1,1), (s,0),
(0,t), per tutti i reali s e t. La
natura del primo punto critico si risolve subito con
l'Hessiano, concludendo che si tratta di un massimo. Negli
altri punti l'Hessiano è nullo e quindi bisogna fare
uno studio locale. Trattiamo esplicitamente il caso dei punti
(0,t), gli altri si risolvono in maniera analoga.
E' utile eseguire la traslazione di assi
. Si trovano
facilmente i seguenti punti critici (1,1), (s,0),
(0,t), per tutti i reali s e t. La
natura del primo punto critico si risolve subito con
l'Hessiano, concludendo che si tratta di un massimo. Negli
altri punti l'Hessiano è nullo e quindi bisogna fare
uno studio locale. Trattiamo esplicitamente il caso dei punti
(0,t), gli altri si risolvono in maniera analoga.
E' utile eseguire la traslazione di assi ![]() , che porta i punti critici nell'origine. Per
sostituzione si ottiene
g(h,k)=h2(k+t)
3(6-3t-2h-3k),
g(0,0)=0. A noi interessa dunque il segno di g
per valori di h e k vicini a zero. La
discussione è abbastanza agevole se si considerano
preliminarmente i casi t=0 e t=2.
, che porta i punti critici nell'origine. Per
sostituzione si ottiene
g(h,k)=h2(k+t)
3(6-3t-2h-3k),
g(0,0)=0. A noi interessa dunque il segno di g
per valori di h e k vicini a zero. La
discussione è abbastanza agevole se si considerano
preliminarmente i casi t=0 e t=2.
- t=0. g(h,k)=h2k 3(6-2h-3k). La funzione risulta essere il prodotto di tre fattori, di cui il primo è positivo, il secondo non ha segno costante, il terzo è positivo (per la presenza del 6). La funzione non ha né massimo né minimo.
- t=2. g(h,k)=h2(k+ 2)3(-2h-3k). La funzione risulta essere il prodotto di tre fattori, di cui il primo è positivo, il secondo anche (per la presenza del due), il terzo non ha segno costante (è positivo su un semipiano e negativo sull'altro tra quelli individuati dalla retta -2h-3k=0). La funzione non ha né massimo né minimo.
- t<0. La funzione risulta essere il prodotto di tre fattori, di cui il primo è positivo, il secondo negativo, il terzo positivo. Si ha dunque un massimo.
- 0<t<2. La funzione risulta essere il prodotto di tre fattori, tutti positivi. Si ha dunque un minimo.
- t>2. La funzione risulta essere il prodotto di tre fattori, di cui il primo è positivo, il secondo positivo, il terzo negativo. Si ha dunque un massimo.