Superfici di rotazione
Le superfici di rotazione si ottengono ruotando una curva γ, detta curva meridiana, attorno ad una retta a, detta asse di rotazione.
Fissato un punto P di γ, consideriamo il piano π passante per P ed ortogonale alla retta a; indichiamo con C l'intersezione tra π ed a e con r la distanza tra C e P. L'intersezione tra la sfera S di centro C e raggio r e il piano π individua esattamente la circonferenza descritta dal punto P nella sua rotazione attorno ad a. Questa considerazione fornisce un metodo per determinare l'equazione della superficie di rotazione.
Se infatti la curva γ è data mediante le equazioni parametriche γ = (x(t), y(t), z(t)), abbiamo le coordinate di P in funzione di t. Data poi l'equazione di a, è facile trovare il piano π (la cui equazione dipenderà da t), le coordinate di C (sempre in funzione di t), la distanza CP e l'equazione della sfera S. Il sistema tra l'equazione di S e quella di π fornisce l'equazione della circonferenza che, al variare di P sulla curva γ individua la superficie: basterà eliminare il parametro t per averne l'equazione cartesiana.
Esempio. Sia data la curva meridiana γ =
(t, 2, t) (è una retta), e l'asse
di rotazione a = (u, 1, 3). Il piano π ha
equazione cartesiana 1(x-t) + 0(y-2) +
0(z-t) = 0, cioè x - t = 0. Il punto
C ha dunque coordinate (t, 1, 3) e la distanza
CP, cioè il raggio della sfera S, 
. L'equazione della circonferenza richiesta è
allora data dal sistema 
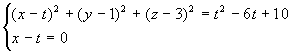, che, per
eliminazione di t fornisce l'equazione cartesiana
cercata: x2 - y2 -
z2 - 6x + 2y + 6z
= 0.
L'immagine qui sotto, che può essere ruotata, mostra la figura risultante.
Per le applicazioni interessa spesso il caso particolare in cui
la superficie è ottenuta per rotazione, attorno ad uno
dei due assi coordinati, di una curva (di solito grafico di una
funzione) tracciata in un piano cartesiano. Per chiarire il
concetto consideriamo, in un piano uz, con u
≥ 0, una curva f(u,z) = 0 e immaginiamo di
ruotarla di 360° attorno all'asse z. Un punto
P(u,z) della curva, ruotando, descrive una
circonferenza con centro nel punto (0,z). Il semiasse
positivo delle u descriverà un piano che
sarà il piano xy del sistema xyz in cui
rappresentiamo la superficie di rotazione, ed è evidente
che si dovrà avere 
. L'equazione
della superficie si potrà dunque ottenere operando
semplicemente questa sostituzione nell'equazione
f(u,z) = 0. Discorsi simili se vogliamo
ottenere una superficie di rotazione attorno all'asse
x o y: basterà considerare curve nei
piani ux o uy rispettivamente. Mostriamo due
esempi per chiarire il concetto: il primo si riferisce alla
funzione seno, nel tratto tra 0e 2π, il secondo alla funzione
logaritmo, nel tratto tra 0 e 5. Le immagini possono essere
ruotate.