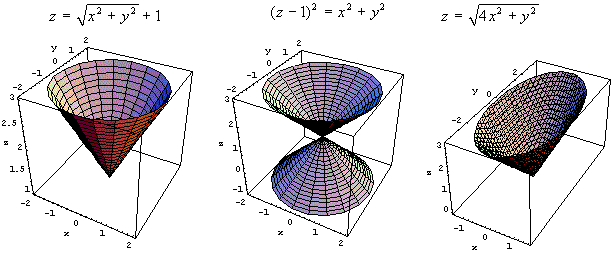Analisi due - Alcuni grafici di superfici 3D
Proponiamo in questa pagina alcuni grafici di superfici 3D, di uso comune quando si studiano funzioni di più variabili. Naturalmente ci limitiamo solo ad alcuni esempi estremamente semplici, utili per iniziare a familiarizzare con grafici tridimensionali. Segnaliamo che è opportuno non farsi ingannare dalla (relativa!) semplicità dei casi qui presentati: le superfici 3D possono presentare situazioni estremamente complesse, ovviamente ancora più complesse di quanto non succeda per le curve nel piano!
Piani
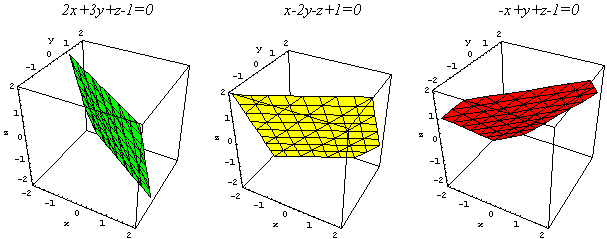
I piani di R3 hanno equazioni del tipo ax+by+cz+d=0. Se c ≠ 0 si possono scrivere, esattamente come le rette nel piano, in forma "esplicita": z = mx+ny+q. Se nell'equazione "manca" un'incognita il piano è parallelo al rispettivo asse, se mancano due incognite, il piano è parallelo al rispettivo piano coordinato. Per rendersi conto della disposizione spaziale del piano è utile, spesso, tracciarne le intersezioni con i tre piani coordinati. Proponiamo alcuni esempi.
Superfici di
rotazione 
Sfera con
centro in (xC, yC,
zC). Ha equazione:
(x-xC)2+(y-y
C)2+(z-zC)2=
r2, cioè praticamente lo stesso tipo
già incontrato per la circonferenza in due dimensioni.
Ellissoidi con assi paralleli agli assi
coordinati. Hanno equazioni del tipo:
a(x-xC)2+b(y-
yC)2+c(z-zC)
2=1, con a,b,c costanti positive. Se due di queste
costanti sono uguali si tratta di un ellissoide di rotazione. Le
tre figure qui sotto si riferiscono a ellissoidi con centro
nell'origine e coefficienti a,b,c dati, rispettivamente, da
(2,1,3), (2,1,⅓), (⅓,1,⅓). Solo l'ultimo
è una figura di rotazione (attorno all'asse
y), come è reso evidente anche dal tipo di
rappresentazione grafica adottata.
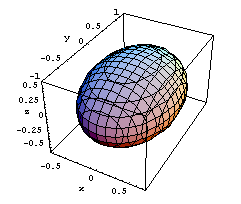
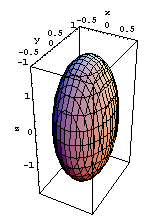
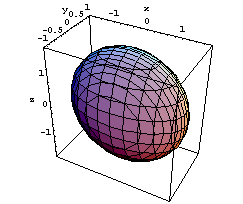
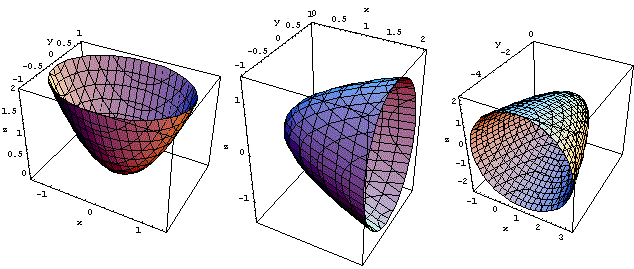
Paraboloidi. Hanno equazioni di vario tipo, a
seconda di come sono originati a partire da una parabola in un
piano. I più comuni sono quelli del tipo z =
a(x-xV)2+b(y-
yV)2 +zV (o
analoghi scambiando gli assi). Le figure qui sotto si
riferiscono ai paraboloidi z = x2 +
2y2, x = 2y2
+ z2, y =
-(x-1)2 - z2, dei
quali l'ultimo è di rivoluzione.
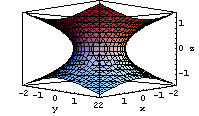
In sostanza si tratta di partire da una parabola z=(t-tV)2 + zV in un piano tz (e analogamente scambiando z con x o y), eseguire una rotazione attorno all'asse z e poi eventualmente cambiare i coefficienti per ottenere una superficie a sezioni ellittiche. Con questa tecnica si possono ottenere altri paraboloidi eseguendo una rotazione di parabole del tipo t = z2. Qui sotto, a mo' d'esempio, è rappresentata la figura che si ottiene ruotando la parabola t = z2+1, che produce la superficie x2 + y2 - z4 - 2z2 - 1 = 0.
Iperboloidi. Anche in questo caso si tratta di
eseguire rotazioni opportune di iperboli in un piano e poi
eventualmente cambiare i coefficienti per ottenere superfici a
sezioni ellittiche. Proponiamo due grafici, a titolo
d'esempio. Il primo si riferisce all'equazione
-x2 + y2 -
z2 = 1, il secondo all'equazione
x2 + 2y2 -
z2 = 1.
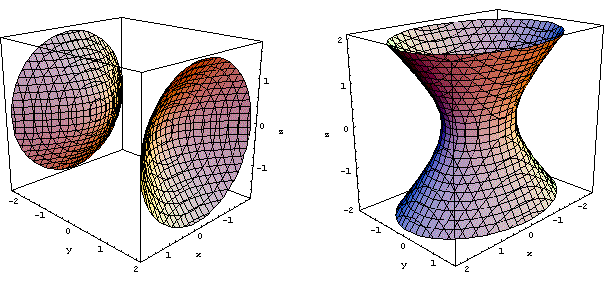
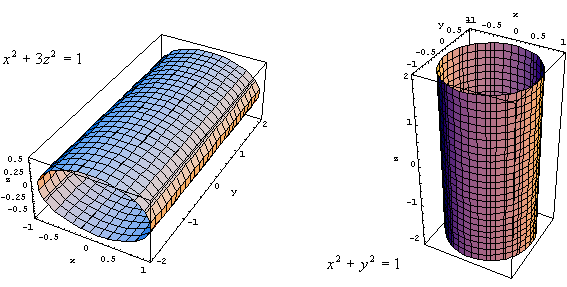
Cilindri.
Interessano in modo particolare i cilindri con asse parallelo ad
uno degli assi coordinati, eventualmente a sezione ellittica.
Anche qui proponiamo due grafici d'esempio.
Coni.
Anche per questo caso la situazione più comune nelle
applicazioni si riferisce a figure con asse parallelo ad uno
degli assi coordinati. Per analizzare questo tipo di superfici
si può ricordare che esse derivano da rotazioni di una
retta attorno ad un'altra, ad essa incidente: in un piano,
tz, per esempio, si può ruotare la retta z =
at + b attorno all'asse z, ottenendo la
superficie z =
a√(x2+y2)+1.
Proponiamo tre figure a titolo d'esempio.
