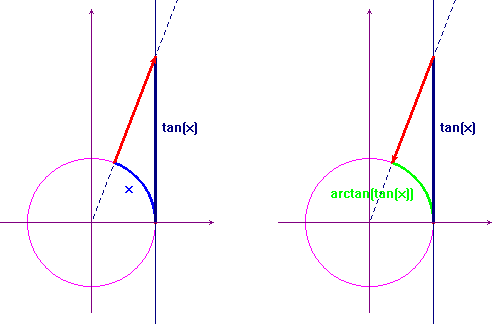
La funzione arctan(tan(x))
La funzione tangente è definita su 
,
e fornisce valori su tutto R; ciò
significa che la funzione arctan(tan(x)) non è
definita su R, e quindi non può essere
l'identità su R; la cosa è
ulteriormente confermata dal fatto che arctangente ha solo
l'intervallo 
come codominio. Se ne
deduce che il fatto che le due funzioni arctangente e tangente
non sono una l'inversa dell'altra ha, in questa
composizione, importanti conseguenze.
Per capire come vanno le cose osserviamo innanzitutto che la
funzione tangente è periodica di periodo π e quindi
basterà limitare l'indagine ad un intervallo ampio
π: poiché l'arctangente è l'inversa
della tangente ristretta a ,sceglieremo proprio
questo intervallo. Basterà invocare le note
proprietà delle funzioni inverse per concludere che
la funzione considerata è semplicemente
l'identità di . La cosa è
provata dinamicamente dall'animazione qui sotto: mentre il
punto P descrive il tratto , il punto R, che
descrive la funzione composta arctanotan, percorre il corrispondente tratto
della bisettrice y=x.
Qui sotto è rappresentato il grafico complessivo, ottenuto per periodicità.
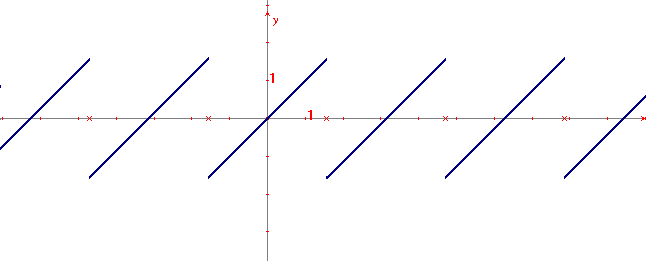
É facile rendersi conto analiticamente del risultato ottenuto dinamicamente.
I due grafici qui sotto riportano la situazione per x
nell'intervallo ; per gli altri x
basta invocare la periodicità della funzione tangente.
