Relazioni d'ordine
La nomenclatura utilizzata dai vari autori in relazione a questa importante classe di relazioni non è univoca ed è opportuno, consultando un testo, controllare sempre qual è la definizione utilizzata.
Diremo relazione d'ordine una relazione che sia transitiva e, in aggiunta,
- riflessiva e antisimmetrica (relazione d'ordine debole o semplicemente d'ordine).
- irriflessiva e asimmetrica (relazione d'ordine forte).
In molti testi una relazione riflessiva, antisimmetrica e transitiva è chiamata ordine parziale. (In inglese poset è un insieme su cui sia stabilita una relazione d'ordine di questo tipo, detta partial order).
Una relazione che sia riflessiva e transitiva è chiamata un preordine.
Un ordine debole si dice totale o
lineare se, dati due elementi
x ed y, si ha x![]() y
y ![]() y
y![]() x (si noti che se sussistono
entrambe si ha x=y). Analogamente un ordine stretto si
dice totale o lineare se dati due elementi x ed
y, si ha x
x (si noti che se sussistono
entrambe si ha x=y). Analogamente un ordine stretto si
dice totale o lineare se dati due elementi x ed
y, si ha x![]() y
y
![]() y
y![]() x
x
![]() x=y (si noti che, in questo caso, le tre
possibilità sono mutuamente esclusive).
x=y (si noti che, in questo caso, le tre
possibilità sono mutuamente esclusive).
Le relazioni d'ordine (debole) sono abitualmente indicate
con simboli come ≤ , ![]() , o simili; quelle di ordine stretto con
<,
, o simili; quelle di ordine stretto con
<, ![]() , o simili.
, o simili.
Le relazioni d'ordine permettono di introdurre i concetti di massimo e minimo, di enorme importanza nelle applicazioni.
Esempi
- L'unica relazione di equivalenza che sia anche di ordine (debole) è l'uguaglianza.
-
La relazione, in R, x
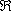 y se e solo se
x2 ≤ y2 è
un preordine (non vale la proprietà antisimmetrica: si
ha -2
y se e solo se
x2 ≤ y2 è
un preordine (non vale la proprietà antisimmetrica: si
ha -2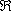 2 e
2
2 e
2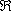 -2,
ma -2≠2).
-2,
ma -2≠2).
-
La relazione
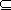 ,
nell'insieme delle parti di un insieme è un ordine
(debole), che non è totale.
,
nell'insieme delle parti di un insieme è un ordine
(debole), che non è totale.