Relazioni di equivalenza
Una relazione 
si
dice di equivalenza se
è:
- riflessiva
- simmetrica
- transitiva
Le relazioni di equivalenza giocano un ruolo molto importante
nei campi più svariati. Il motivo è
sostanzialmente legato al seguente fatto. Consideriamo un
insieme A su cui sia stabilita una relazione di
equivalenza. Per ogni x di A indichiamo con
[x] l'insieme di tutti gli elementi di A
che sono in relazione con x: [x] = {y 
A | xy}. L'insieme [x] è detto
classe di equivalenza di x
L'insieme {[x] | x A}
è di solito indicato con A/, si chiama insieme quoziente di A rispetto ad
, e
gode delle seguenti importanti proprietà:
- I suoi elementi (che sono sottoinsiemi di A) sono non vuoti.
- Due suoi elementi distinti sono disgiunti (come sottoinsiemi di A).
-
.
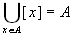La dimostrazione è abbastanza semplice e può costituire un utile esercizio sulle relazioni.
Dato un insieme A, una famiglia F di suoi
sottoinsiemi con le tre proprietà appena enunciate si
chiama una partizione di
A. Possiamo dunque concludere che una relazione di equivalenza
su un insieme A individua una partizione di A.
Viceversa data una partizione F di A, la
relazione xy se e solo se x ed y
appartengono allo stesso sottoinsieme della partizione è
una relazione di equivalenza in A. Esiste quindi una
corrispondenza biunivoca tra relazioni di equivalenza e
partizioni di un insieme.
In sostanza l'introduzione su un insieme di una relazione di equivalenza equivale a raggruppare gli elementi di A in modo che ogni gruppo contenga tutti gli oggetti che si equivalgono. Il gruppo, sotto molti aspetti, può essere trattato come un unico oggetto.
Esempi
- Nell'insieme di tutte le rette dello spazio la relazione "essere parallelo" è di equivalenza, le classi di equivalenza sono costituite dai fasci di rette parallele e queste classi di equivalenza si chiamano anche direzioni: la direzione di una retta è quella cosa che hanno in comune tutte le rette tra di loro parallele.
-
Se p è un naturale, la relazione in
Z: x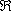y se e solo se x-y
è multiplo di p, è una relazione di
equivalenza, che si chiama congruenza modulo p e si
indica con ≡p. Il suo insieme quoziente
è costituito da p elementi, e precisamente:
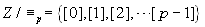. Su questo insieme si può
introdurre un'aritmetica con proprietà molto
interessanti.
-
In un insieme di due elementi A={x,y} le
uniche relazioni di equivalenza sono 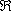1={(x,x),(y,y)} ed 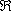2=A×A.
- In un insieme di tre elementi le possibili relazioni di equivalenza sono le seguenti:
-
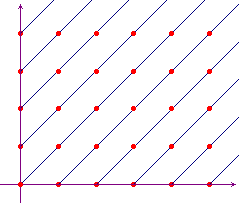
Nell'insieme N×N
la relazione (n,m)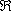(p,q) se n+q=m+p è una relazione di
equivalenza, le cui classi di equivalenza sono costituite da
tutti e soli i punti che appartengono a semirette parallele
alla bisettrice del I e III quadrante. Nell'insieme
quoziente si possono introdurre le operazioni di somma e
prodotto e si ottiene un gruppo abeliano rispetto alla somma:
è l'insieme degli interi. La bisettrice del primo
e terzo quadrante gioca il ruolo di zero, le semirette al di
sotto giocano il ruolo di interi positivi, quelle al di sopra
di interi negativi.
