Integrazione per sostituzione 
La regola di derivazione delle funzioni composte ha come conseguenza una importante tecnica per il calcolo delle primitive, detta integrazione per sostituzione.
Si debba calcolare 
e si consideri una
funzione g(t), derivabile, con derivata continua e
sempre diversa da zero; si indichi con h(x) la sua
funzione inversa. Si consideri l'integrale 
e sia F(t) una sua primitiva. Allora si ha 
.
Se usiamo la "scrittura con il dx" per l'integrale
e ricordiamo una suggestiva forma per la scrittura del
differenziale di una funzione [d(g(t)=g'(t)dt],
possiamo memorizzare facilmente questo teorema nel seguente
modo: per calcolare 
esegui la sostituzione x=g(t) sia nella
variabile della f che nel "dx"; se ottieni un
integrale facilmente calcolabile, allora per avere le primitive
della funzione originale devi eseguire la sostituzione inversa
t=g-1(x).
Naturalmente il problema nell'uso di questa tecnica è quello di "indovinare" la sostituzione giusta, cosa tutt'altro che facile. In ogni caso, come già detto altre volte, non vale la pena di perdere troppo tempo per diventare esperti in questo campo. Per questo motivo proporremo solo alcuni esempi semplici, o che rivestono speciale interesse, per chiarire il metodo.
Esempi
-
Calcolare
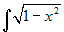. Posto x =
sint si ottiene t=arcsinx,
x' = cost e si deve calcolare
l'integrale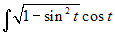 
. Si ottiene:
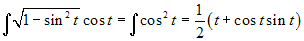. Operando la sostituzione inversa
si ricava: 
.
-
Calcolare
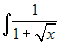. Posto 
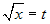, si ottiene x = t2,
x' = 2t e si deve calcolare l'integrale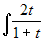 
. Si ottiene: 
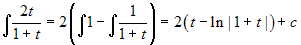. Allora 
.
-
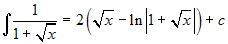Calcolare
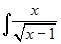. Posto 
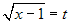, si ottiene x =
1+t2, x' = 2t e si
deve calcolare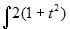 
. Si ha: 
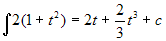. Allora 
.
-
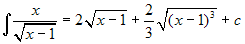La "scrittura con il dx" può essere utile
anche in un altro modo. Sia, per esempio, da calcolare
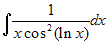. Se poniamo lnx = t,
otteniamo: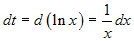 
. L'integrale dato
si trasforma subito in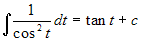 
. Si ha allora 
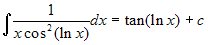. Questo
integrale poteva comunque essere calcolato anche
semplicemente usando la regola delle funzioni composte.
Spesso però l'uso della regola di sostituzione
facilita la ricerca della via più breve per trovare le
primitive.