Integrazione "per parti" 
Una semplice rilettura della regola di derivazione del prodotto di due funzioni fornisce subito la seguente regola, detta di integrazione per parti:
Siano date due funzioni f e g, e sia
F una qualunque primitiva di f. Si ha allora:
.
La formula si può leggere nel seguente modo: dato il prodotto di due funzioni f e g, e data una primitiva F della prima funzione, una primitiva del prodotto si trova facendo il prodotto della primitiva F della prima funzione per la seconda (fin qui in modo simile alla derivata di un prodotto), meno una primitiva del prodotto tra la primitiva F della prima e la derivata della seconda (e questa seconda parte è completamente diversa dalla regola sulla derivata di un prodotto).
Ci sono altri modi per scrivere, e leggere, questa formula: noi preferiamo quello indicato perché, vista la somiglianza con la regola della derivata di un prodotto, è forse il più semplice da memorizzare.
Osservazioni ed esempi importanti
-
La formula indicata non risolve il problema del calcolo delle
primitive di un prodotto: sposta solo il problema dal
prodotto fg al prodotto Fg'. Il suo uso
sarà conveniente solo se la ricerca delle primitive di
Fg' è più semplice che non quella
delle primitive di fg.
Esempio.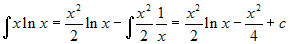
.
-
Anche se il prodotto fg è uguale al prodotto
gf, la formula non è simmetrica rispetto alle
due funzioni f e g: scambiando l'ordine
tra le due funzioni si è ricondotti alla ricerca di
primitive diverse, Fg' oppure Gf'
(con ovvio significato dei simboli), e può benissimo
succedere che una delle due ricerche sia facile, mentre
l'altra no.
Esempio.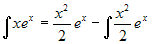
e
quest'ultimo integrale è più difficile di
quello di partenza. Cambiando l'ordine si ottiene invece:
-
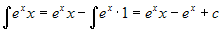
A volte la formula si applica anche in presenza di una sola
funzione, osservando che f =
1·f.
Esempio.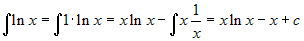
.
-
Naturalmente non è escluso che la formula debba essere
applicata di nuovo per calcolare la primitiva residua di
Fg'.
Esempio.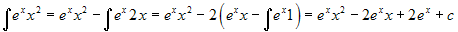
(attenzione ai
segni!!).
-
La maggiore difficoltà nell'uso della formula
è comunque legata al fatto che non è detto che
essa debba essere sempre applicata nel caso di un prodotto di
due funzioni.
Esempio. Per calcolare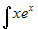
si deve utilizzare la formula per parti, mentre 
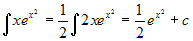, utilizzando la regola sulle funzioni
composte.
-
Una particolare tecnica si usa quando, applicando
ripetutamente la formula per parti, si ritorna al punto
iniziale.
Esempio.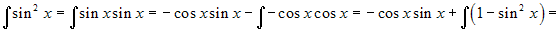
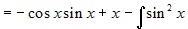. Da qui si trova subito 
.
-
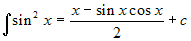Si osservi che se, dopo ripetute applicazioni della formula
per parti, si ottenesse
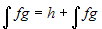, si dovrebbe concludere che h è una
funzione costante, non necessariamente nulla. Per esempio la
scrittura 
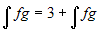è perfettamente
legittima.
Altri esempi
-
.
-
.
-
.
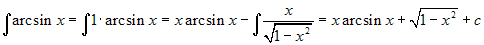
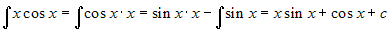
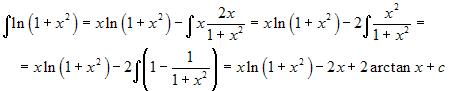