Applicazioni del calcolo infinitesimale
Per essere esaustiva questa pagina dovrebbe comprendere una gran mole dei contenuti di moltissime discipline: fisica, biologia, chimica, ecologia, economia, elettronica, meccanica, ecc.... Qui intendiamo invece proporre solo alcune tra le applicazioni più elementari delle tecniche del calcolo infinitesimale.
La tangente ad una curva
Si tratta della applicazione più naturale, in quanto il concetto di derivata nasce proprio dal problema della ricerca delle tangenti al grafico di una funzione.
Se è data una funzione 
,
dove I è un intervallo di R, e se
c è un punto di I dove la funzione è
derivabile, la retta tangente al grafico della funzione nel
punto (c , f(c)) esiste ed ha equazione: y =f(c)
+ f'(c)(x - c).
La tecnica di derivazione può essere applicata anche alle curve che non siano grafici di funzioni. Si consideri per esempio la circonferenza di centro l'origine e raggio 1: x2 + y2 = 1, e si supponga di volerne trovare la tangente nel punto del primo quadrante di ascisse 1/3. Si possono usare i metodi elementari (retta perpendicolare al raggio o metodo del "Δ=0"), ma si può anche ragionare nel seguente modo:
-
in un intorno del punto in questione la circonferenza
coincide con il grafico della funzione
;
-
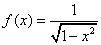la derivata di questa funzione è:
;
-
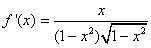se ne deduce che il coefficiente angolare della tangente
cercata è:
.
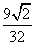Il problema della ricerca delle tangenti a curve definite da equazioni in due incognite, f(x,y) = 0, è di grande importanza importanza applicativa e viene affrontato utilizzando il Teorema del Dini, la cui formulazione esula però dagli scopi di questa monografia.
Velocità e accelerazione
Si consideri un punto P, mobile su una retta su cui si sia fissato un sistema di ascisse. L'ascissa x del punto è allora una funzione del tempo t, e la conoscenza di questa funzione, x = f(t), determina completamente il moto. Come è noto, si usa abitualmente la scrittura x = x(t), al posto di x = f(t), per evitare il proliferare dei simboli. Le derivate prima e seconda di questa funzione misurano, rispettivamente, la velocità e la accelerazione (scalari) del punto P:
v = f'(t) = x'(t) a = f"(t) = x"(t)
Molti testi usano ancora la notazione di Newton: 
, al posto di x',
x".
Identiche considerazioni si possono fare nel caso di un moto su traiettoria prestabilita, fissando un sistema di ascisse curvilinee sulla traiettoria stessa. Abitualmente si usa in questo caso la notazione s = s(t), e conseguentemente per la velocità e accelerazione v = s'(t), a = s"(t).
Si parlerà (sia per i moti rettilinei che su traiettoria prestabilita) di moto uniforme se la velocità v è costante, di moto uniformemente accelerato se la accelerazione a è costante.
Nel caso di moto in due dimensioni si introdurrà un sistema di coordinate cartesiane nel piano e il moto sarà individuato da due funzioni del tempo, che sono le componenti del vettore posizione. Si usano le seguenti notazioni:
.
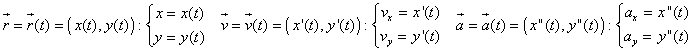Come è noto, si dimostra:
- che il vettore velocità è tangente alla traiettoria;
-
che per il modulo del vettore velocità vale:
;
-
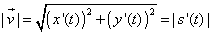che il vettore accelerazione ha due componenti, una tangente
alla traiettoria (detta appunto accelerazione tangenziale) e
una perpendicolare alla traiettoria (detta accelerazione
centripeta):
;
-
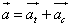che il modulo del vettore accelerazione non
coincide con il modulo dell'accelerazione scalare, e si
ha, invece:
-
;
-
.
-
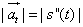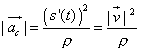Intensità di corrente elettrica
Consideriamo un conduttore percorso da corrente, una sua sezione dS, e la carica q che la attraversa. Questa carica è naturalmente una funzione del tempo: q = q(t). La derivata di questa funzione (a meno del segno) prende il nome di intensità di corrente elettrica:
i = q'(t).
Nel caso che la derivata sia costante la corrente si dice continua.
Problemi di massimo e minimo
Si tratta di una delle applicazioni fondamentali del calcolo differenziale, che ha applicazioni in tutti i campi. Si tratta di trovare il massimo o il minimo di una funzione quando la o le variabili assumono valori appartenenti ad un certo insieme. Alcuni esempi chiariranno il significato di questa affermazione:
- Tra tutti i triangoli di dato perimetro trovare quello di area massima.
- Tra tutti i solidi di dato volume trovare quello che ha la minima superficie totale.
- Trovare la massima distanza raggiungibile da un proiettile che viene lanciato con una data velocità iniziale.
- Trovare il percorso di minimo tempo che faccia passare un raggio di luce da un punto A di un mezzo ad un punto B di un altro mezzo.
- ...
Non esistono strategie generali per risolvere questo tipo di problemi, che spesso sono molto complessi. Nei casi più elementari si tratta di rendere massima o minima una certa quantità, i cui valori dipendono da un parametro, variabile in un determinato insieme di valori. Il problema si matematizza scrivendo la regola che esprime la quantità da massimizzare o minimizzare in funzione del parametro, e applicando il calcolo differenziale per trovare i valori massimo o minimo.
Esempio. Si deve far passare una lastra rettangolare in un corridoio di larghezza h, formante un angolo retto. Trovare la massima lunghezza ammessa per la lastra.
É chiaro che si riscontreranno problemi solo nel superare l'angolo retto e che la migliore soluzione sarà di disporre la lastra come nella figura, dove è rappresentata la pianta del corridoio.
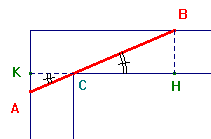
Assunto come parametro l'angolo indicato in figura, si
tratterà di trovare l'angolo per cui AB è
minimo: questo minimo corrisponderà alla massima
lunghezza ammessa per la lastra. Detto x
quest'angolo si ha: AB = AC + CB = 
.
Derivando si trova subito che l'angolo che corrisponde al
minimo è quello di π/4 e da qui si ottiene il valore
richiesto.
Il problema è molto semplice (e si poteva risolvere anche a livello "intuitivo"), ma è istruttivo perché, mentre il problema chiede un valore massimo, tecnicamente bisogna trovare un minimo.