www.batmath.it

La rappresentazione decimale dei reali

L'origine del problema

Consideriamo una famiglia di conigli salterini, tale che il capostipite può fare salti solo di una determinata lunghezza, mentre i discendenti possono effettuare solo salti lunghi la metà del rispettivo padre. Supponiamo che i salti del capostipite siano come nel segmento CD della figura qui sotto e che la famiglia dei conigli si ponga il seguente problema: partendo da un certo punto A quanti salti deve fare ciascuno per arrivare ad un punto B fissato, con la regola che ciascun discendente può partire solo dopo che il rispettivo padre ha compiuto tutti i salti che era in grado di fare, e con la condizione di non superare mai B.

Nell'esempio di figura  il capostipite salterà due volte. Anche se dall'esame della figura risulta evidente che con un opportuno numero di salti il capostipite può sempre superare B, la cosa non è del tutto banale: si tratta della proprietà archimedea dell'insieme dei numeri reali, così chiamata in onore di Archimede che comprese che si trattava di una proprietà essenziale della retta e la enunciò esplicitamente come uno degli assiomi della geometria. E' come dire che anche un piccolo regolo usato un numero sufficiente di volte può misurare distanze arbitrariamente grandi. Se il capostipite non è stato in grado di raggiungere esattamente B, facciamo partire il figlio, poi il nipote, e così via. Procedendo in questo modo potremo arrivare sempre in B?. Come è noto è merito di Pitagora e della sua scuola l'aver scoperto che la risposta è negativa, in particolare per il caso in cui AB è la diagonale di un quadrato e CD è il suo lato. Si badi bene che non è possibile dare una giustificazione grafica di questa impossibilità: da un punto di vista pratico ad un certo punto un coniglio arriverà così vicino a B da non poter decidere se ci sta sopra oppure no. Si noti altresì che, mentre il capostipite può compiere anche un numero molto grande di salti, i suoi discendenti possono compierne solo 1 o nessuno (d'altra parte altrimenti che capostipite sarebbe?). Si usa memorizzare questo fatto in maniera compatta scrivendo prima il numero di salti del capostipite, e separati da una virgola o da un punto, il numero di salti dei discendenti, scrivendoli uno accanto all'altro. La loro posizione nella stringa indicherà anche il livello di discendenza del saltatore, se avremo l'accortezza di scrivere zero quando un discendente non ha saltato (si tratta in sostanza di un'estensione del sistema posizionale che abbiamo già usato per gli interi.). Naturalmente invece di imporre ai discendenti di saltare una lunghezza pari alla metà del progenitore potevamo scegliere un sottomultiplo qualunque: come è naturale sceglieremo il numero che abbiamo usato come base per scrivere i numeri interi, abitualmente il numero dieci, e la scrittura citata la chiameremo allineamento decimale. In questo caso i conigli discendenti possono fare al massimo 9 salti.

Allineamenti decimali

Per semplicità faremo riferimento alla base b=10 (cioè supponiamo che i conigli discendenti saltino un decimo del progenitore) anche se tutti i discorsi sono validi qualunque sia la base. Cominciamo a considerare un reale x[0,1[ (il coniglio capostipite, per il momento, può riposare, dopo aver dato origine ad una così numerosa progenie!). Vale il seguente

Teorema 1:
Esiste una ed una sola successione a₁, a₂, ..., a_n, ... di interi dell'intervallo [0,9] tali che, per ogni intero n≥1 si ha: 

  (**)

In termini di conigli salterini il teorema si può così enunciare: qualunque sia il livello, n, di discendenza a cui vogliamo arrivare, o ci sarà un discendente che è saltato esattamente sopra x e allora i successori non dovranno neppure scomodarsi, oppure il salto dell'ultimo discendente (di lunghezza 1/10ⁿ), lo avrà portato così vicino ad x che un ulteriore salto, per quanto possa essere piccolissimo se n è molto grande, lo porterebbe al di là di x. Il teorema è intuitivamente abbastanza evidente e puoi vederne la dimostrazione.

É chiaro che se uno dei discendenti è riuscito ad arrivare proprio su x avremo , altrimenti x si potrà ottenere come somma di una serie .

La successione di numeri a₁, a₂, ..., a_n, ...così ottenuta a partire da x si indica con 0,a₁a₂...a_n... (ove lo "0," è legato al fatto che il nostro numero è minore di uno). Nel caso che uno dei discendenti sia riuscito a saltare proprio su x, considereremo ugualmente infinita la successione, ponendo uguali a zero tutti i termini successivi all'ultimo salto, in accordo con il fatto che da un certo livello in poi i conigli non hanno più avuto bisogno di saltare. Esiste un'unica importante limitazione al tipo di successioni che si possono ottenere con questo procedimento, limitazione espressa dal seguente teorema:

Teorema 2:
La successione (a_i) non può essere costantemente uguale a nove da un certo punto in poi.

Puoi vedere dimostrazione di questo teorema.

Si può ora dare la seguente

Definizione: Una successione a₁, a₂, ..., a_n, ...di interi dell'intervallo [0,9] si dice un allineamento decimale. Tale allineamento decimale si dice proprio se non è costantemente uguale a nove da un certo punto in poi. Indicheremo l'insieme di tutti gli allineamenti decimali con D, l'insieme di tutti gli allineamenti decimali propri con DP.

A questo punto siamo pronti per un ulteriore importante risultato che ci schiude la possibilità di rappresentare i reali medianti allineamenti decimali:

Teorema 3:
La funzione , che a x [0,1[ associa il suo allineamento decimale proprio, è una biiezione.

Omettiamo la dimostrazione di questo teorema che richiede sostanzialmente l'uso delle proprietà dell'estremo superiore nei reali.

Tra tutti gli allineamenti decimali, propri o no, hanno un particolare interesse quelli che, da un certo punto in poi, sono costituiti da un gruppo di cifre che si ripete costantemente. Questo tipo di allineamenti decimali li chiameremo periodici e, se indichiamo con  a_p, a_p+1, ..., a_p+h-1, il primo di questo gruppo di cifre che si ripetono, chiameremo antiperiodo dell'allineamento decimale l'eventuale sequenza di cifre a₁a₂...a_p-1, mentre chiameremo periodo dell'allineamento decimale la sequenza di h cifre a_pa_p+1...a_p+h-1. Nel caso non esista antiperiodo parleremo di decimali periodici semplici, altrimenti di decimali periodici misti. Useremo per questi speciali allineamenti decimali una delle scritture: 

(la seconda ha il vantaggio di non avere soprassegnature, lunghe da realizzare in stampa, ma la prima è di gran lunga la più usata). Gli allineamenti decimali impropri sono quelli che hanno periodo nove, mentre quelli che hanno periodo zero si usano chiamare allineamenti decimali finiti e in questo caso, di solito, la scrittura del periodo si omette.

É molto importante il seguente teorema che giustifica l'enorme importanza del sottoinsieme degli allineamenti decimali periodici nell'insieme di tutti gli allineamenti decimali:

Teorema 4:
La biiezione considerata nel teorema precedente induce una biiezione tra l'insieme dei razionali dell'intervallo [0,1[ e gli allineamenti propri periodici.

La semplice dimostrazione di questo teorema è basata sull'algoritmo per calcolare la frazione generatrice di un decimale periodico.

    Occupiamoci ora degli allineamenti decimali impropri. Per chiarire il loro ruolo nell'insieme di tutti gli allineamenti decimali, consideriamo la funzione che ad ogni allineamento decimale fa corrispondere il reale x dell'intervallo [0,1] (attenzione ora anche l'uno è compreso!) ottenuto coma somma o eventualmente come serie nel seguente modo: . Vale il seguente teorema, di cui diamo solo l'enunciato:

Teorema 5:

• Se 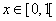è un razionale espresso da una frazione ridotta ai minimi termini del tipo 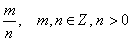, in cui n, scomposto in fattori, contiene solo i fattori 2 e 5, allora x è, nella funzione φ, immagine di due allineamenti, uno proprio, con periodo zero, e l'altro improprio, cioè con periodo nove.
• Se x=1, allora x è immagine solo dell'allineamento improprio .
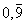• Tutti gli altri x di [0,1[ sono immagini di un unico allineamento decimale proprio. In particolare gli irrazionali sono immagini di un allineamento decimale non periodico, i razionali di un allineamento decimale periodico.

Se ora x è un reale positivo, possiamo osservare che x=[x]+x-[x]; ora 0≤x-[x]<1, mentre [x] è un intero che si rappresenta, con la scrittura decimale, con una successione di cifre: c_kc_k-1...c₀. Utilizzando la scrittura decimale di x-[x] si avrà allora: x=c_kc_k-1...c₀+0,a ₁a₂...a_n...Si usa scrivere, in maniera compatta, x=c_kc_k-1...c₀ ,a₁a₂...a_n... e anche questa scrittura si chiama un allineamento decimale. Per scrivere anche i numeri negativi basta solo utilizzare, a questo punto, il segno meno.

In sostanza possiamo concludere che ogni reale può essere rappresentato utilizzando gli allineamenti decimali, prestando attenzione al fatto che certi razionali ne hanno due di allineamenti decimali, uno proprio e uno improprio.

Conclusioni

Tenendo anche conto di un risultato elementare sulla rappresentazione decimale dei razionali, risultato di semplice dimostrazione, possiamo trarre le seguenti conclusioni, relativamente alla rappresentazione decimale di un numero reale x.

1. Se x è un numero razionale allora una sua rappresentazione decimale è sempre periodica, eventualmente con periodo zero, nel qual caso si dice finita. Inoltre, se il razionale è espresso da una frazione, ridotta ai minimi termini,  del tipo :
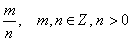   • Se il denominatore è uno (numero intero) oppure se, scomposto in fattori, contiene solo i numeri 2 e 5, il numero può essere rappresentato con due allineamenti decimali di cui uno finito e uno improprio, cioè con periodo 9. Il numero razionale si dice anche numero razionale decimale (in considerazione del fatto che si può ridurre ad una frazione equivalente avente per denominatore una potenza di dieci, eventualmente 10⁰, se si tratta di un intero).
   • Se il denominatore, scomposto in fattori, contiene solo fattori diversi da 2 e da 5, il numero può essere rappresentato con un unico allineamento decimale periodico semplice.
   • Se il denominatore, scomposto in fattori, contiene sia uno dei fattori 2 o 5, che altri fattori, il numero può essere rappresentato con un unico allineamento decimale periodico misto.
2. Se x è un reale irrazionale allora può essere rappresentato con un unico allineamento decimale non periodico, o, come si usa dire, illimitato non periodico.

Per ottenere la rappresentazione decimale propria di un reale razionale è sufficiente eseguire la divisione tra il numeratore e il denominatore, arrestando il procedimento non appena si ottiene resto zero (decimale finito o periodico con periodo zero) oppure non appena un resto si ripete. Se il decimale ottenuto è finito, per ottenere la seconda rappresentazione decimale del numero basta ricordare che è la rappresentazione decimale impropria di 1, cioè, in sostanza, che "9 periodico" equivale a far aumentare di 1 la cifra immediatamente precedente il periodo 9. Per esempio . Per contro non esiste alcun metodo elementare per trovare la rappresentazione decimale di un reale irrazionale ed uno dei "passatempi di moda" è quello di trovare un sempre più elevato numero di cifre decimali di numeri importanti per la matematica, come per esempio π ed e.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 10/12/2001 - ultimo aggiornamento il 01/09/2003