Il teorema fondamentale dell'algebra
Consideriamo un polinomio P(z) = anzn+an-1 zn-1+...+a1z+ a0 (n≥1, an≠0). Come è noto si chiama radice del polinomio un numero complesso w che annulla il polinomio.
Il teorema fondamentale dell'algebra afferma che ogni polinomio del tipo citato ha almeno una radice (reale o complessa).
La dimostrazione di questo teorema esula dagli scopi di queste pagine, ma segnaliamo che si tratta di un teorema di fondamentale, tanto che la sua validità nell'insieme dei complessi è uno dei motivi che rendono questo insieme numerico così importante.
Interessiamoci ora di qualche conseguenza di questo teorema.
Se P(z) è un polinomio di grado n, e z1 è una sua radice, per il teorema di Ruffini avremo P(z) = (z-z1)Q1(z) ove Q1(z) è il polinomio di grado n-1 ottenuto dividendo P per z-z1. Anche Q1(z) è un polinomio e dunque avrà almeno una radice, per cui potremo scrivere P(z) = (z-z1)(z-z2)Q 2(z). Iterando il procedimento potremo concludere che il polinomio P si potrà sempre scrivere come il prodotto di una costante (che deve necessariamente essere uguale ad an) per n fattori di primo grado:
P(z) = an(z-z1)(z- z2)(z-z3)···( z-zn)
I numeri z1, z2, ..., zn sono le radici di P(z). Tali radici possono essere tutte diverse o alcune possono essere ripetute. Un esempio banale in cui sono tutte diverse è P(z) = zn-1, in cui le radici sono le n radici n-esime dell'unità; un esempio in cui sono tutte uguali è P(z) = (z-1)n, in cui tutte le radici sono uguali ad 1. Il numero di volte che una radice si ripete si chiama molteplicità della radice stessa. E' ovvio che la somma delle molteplicità di tutte le radici è esattamente n.
E' di particolare interesse il caso in cui i coefficienti
del polinomio siano numeri reali. In questo caso consideriamo
una radice w e la sua complessa coniugata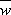 
. Utilizzando le
proprietà del coniugato, e ricordando che il coniugato di
un reale è il numero stesso, si trova:
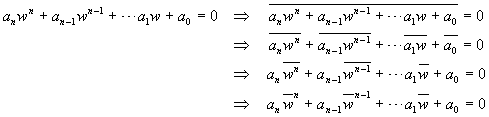
Se ne deduce che anche 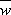è una radice: in un polinomio a
coefficienti reali le radici si presentano sempre a coppie di
radici tra di loro coniugate. Nella decomposizione del
polinomio, se si moltiplicano tra di loro i due fattori che si
riferiscono a radici coniugate si trova 
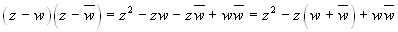, espressione che non
contiene numeri complessi, ma è di secondo grado. Dunque
un polinomio a coefficienti reali si può sempre
decomporre nel prodotto di fattori non contenenti numeri
complessi, al massimo di grado due. Questo fatto ha come
conseguenza che un polinomio di grado dispari, a coefficienti
reali, ha almeno una radice reale.
La decomposizione di un polinomio con la formula sopra riportata ha come conseguenza la decomposizione di un quoziente di polinomi in "fratti semplici".
Consideriamo un esempio per chiarire la situazione. Scomporre il polinomio P(z) = z3-z2+z-1. Si vede subito che esso ha la radice 1. Eseguendo la divisione tra P(z) e z-1 si trova P(z) = (z-1)(z2+1). Le altre due radici sono allora ±i, che sono tra di loro coniugate.