Esponenziali e logaritmi complessi
Proponiamo una breve e informale introduzione alle funzioni elementari nel campo complesso. Una trattazione formale richiederebbe almeno l'uso delle serie di potenze: qui ci limiteremo solo ai concetti essenziali.
La definizione di base, risalente ad Eulero, è la seguente: dato un reale y qualunque, poniamo, eiy = cosy+isiny.
Il numero complesso eiy ha, ovviamente, modulo 1. Considerato poi un complesso z qualunque, z = x+iy definiamo ez come: ez = ex+iy = ex·eiy = ex(cosy+isiny).
E' abbastanza interessante osservare che la funzione ez appena definita è periodica di periodo 2πi; se infatti consideriamo i numeri z e z + 2πi, otteniamo: ez = ex(cosy+isiny), mentre ez+2πi = ex(cos(y+2πi)+isin( y+2πi)) = ex(cosy+isiny) = ez. E' altresì utile notare che la definizione di ez appena data è tale che le usuali proprietà delle potenze rimangono valide. In particolare ci interessa segnalare che ez+w = ez·ew.
Dalla definizione appena data segue una formula famosissima, che contiene tutti e soli i numeri chiave della matematica: 0, 1, e, i, π: eiπ + 1 = 0.
Dalla definizione data segue anche una nuova rappresentazione dei numeri complessi. Se z = x+iy dalla sua forma polare otteniamo z = [ρ,θ] = ρ(cosθ+isinθ) = ρeiθ. La forma così ottenuta si chiama forma esponenziale dei complessi e consente di eseguire facilmente prodotti, ricordando le usuali proprietà delle potenze: z·w = ρeiθ·rei φ. = ρrei(θ+φ).
Procedendo come fatto sui reali si possono ora definire i
logaritmi sui complessi. Purtroppo la già citata
periodicità della funzione esponenziale complica
notevolmente il problema, in quanto non si ha più a che
fare con funzioni biunivoche. Si dà comunque la seguente
definizione: dato un complesso z, si chiama logaritmo (in base e) di z
ogni numero complesso w tale che ew =
z. Si deduce abbastanza facilmente che ogni complesso
z ≠ 0, z = [ρ,θ], ha infiniti
logaritmi, soddisfacenti la seguente proprietà:
z = lnρ + i(θ+2kπ),
k 
Z. Le usuali proprietà dei logaritmi
possono essere estese, seppure con certe limitazioni, anche ai
logaritmi nel campo complesso.
La cosa che ci interessa qui segnalare è che, usando il concetto appena introdotto di logaritmo, si possono definire anche le potenze in C: se z e w sono due complessi qualunque, poniamo zw = ewlnz. Per la potenza così definita si possono estendere le usuali proprietà delle potenze in R, seppure con una certa cautela dovuta al fatto che la funzione logaritmo ha infiniti valori.
Procedendo oltre si possono anche definire le funzioni trigonometriche, mediante le formule:
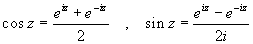
Le funzioni così definite godono di proprietà sostanzialmente simili alle analoghe funzioni in campo reale.
Queste formule sono di grande importanza dal punto di vista teorico, in quanto mostrano che la funzione esponenziale e quelle trigonometriche sono due facce della stessa medaglia. Una trattazione esaustiva e rigorosa delle proprietà di queste funzioni si può trovare in Giovanni Prodi, Analisi Matematica, Boringhieri, Torino 1970: a questo testo rimandiamo per ogni utile approfondimento.