The integral of step functions
Consider a step function 
and a dissection
of [a,b] such that the function
has the constant value ck on each
subinterval of the dissection. Then:
The integral of s from a
to b is the number 
.
This means that the integral is simply the sum of the products of the constants ck times the length of the corresponding subintervals. In particular if f is constant and positive the integral is the area of a rectangle.
The two symbols 
and 
are used without distinction: we prefer the first, or
sometimes 
, because it is more compact, but the
second one has some advantages, in particular when we deal with
multi-variable functions or in the use of the substitution rule.
It is important, at any rate, to remember that the integral
depends only on the function s and the interval
[a,b]: the symbol "dx" has no
particular meaning and is not a differential.
Examples
-
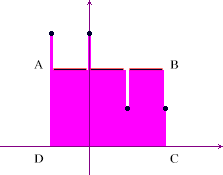
Consider the function
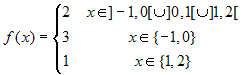. Then the
integral from -1 to 2 is the area of the rectangle ABCD in
the picture here below.
-
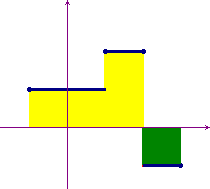
Consider the function
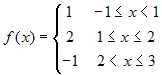. Then the
integral from -1 to 3 is the sum of the areas of the two
yellow rectangles minus the area of the green rectangle.
Observe in particular that the values of the step functions at the points of the dissection are unimportant: these numbers are never used in the previous definition. This means that if you modify the values of a step function in a finite number of points (obviously changing also the dissection of the interval [a,b]) the value of the integral is not affected. This agrees with the fact that the area of a segment is zero. From now on we'll no more graph these points.
It's also important to observe that continuity of the functions is not important for the concept of integral: step functions are never continuous (except when constant!).
In the above definition of integral the number a is
less than b. This definition is usually extended, in
order to allow also a>b, as follows: if a>b then 
. We also define 
.