Step functions
Step functions are functions 
,
that are constant on sub-intervals of [a,b]; they are also
called piecewise constant functions. In order to give a precise
definition of this kind of functions it's useful to
introduce the concept of dissection (or subdivision) of an
interval of real numbers.
A dissection of
an interval [a,b] of real numbers is a set of
n+1 points such that: 
. We'll use the traditional set notation for
dissections: 
.
Given a dissection of [a,b], the interval
[a,b] can be written as 
,
that is as a finite union of subintervals: these subintervals
are generated by the dissection.
Step functions
A function 
is called a
step function on [a,b] if
there exists a dissection D of [a,b] and real
numbers
c1, c2, ... ,
cn, such that, for every k = 1, 2,
... ,n, 
.
Observe that we have imposed no condition on s(xk), except that they are real valued. This is in view of the fact that the Riemann integral is unchanged if we alter the value of the function in a finite number of points.
Examples
-
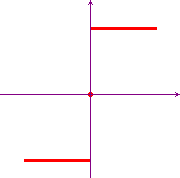
The function f(x)=signum(x), in the
interval [-1,1] is a step function.
-
The function
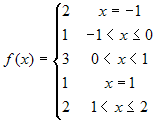is a step function.
-
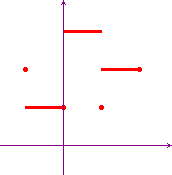
An important example of step function is the following:
f(x)=[x] = "the greatest integer ≤
x". This is a step function on every
interval [a,b] and is called the characteristic
function or the integral part function.
D'. D' is called a refinement of
D. If f is a step function and D is a
dissection of [a,b], the function is constant also in the
subintervals generated by every dissection D' such
that DD'. This means that the
dissection is not uniquely determined by the step function. However
this fact is unimportant for our theory.
Sums and products of step functions
Given two step functions, s and t, and the
corresponding two dissections D and E of their
common domain [a,b], it's a useful exercise to
prove that the two functions s+t and
s·t are step functions and a possible dissection
of [a,b] is simply D
E.
Examples
-
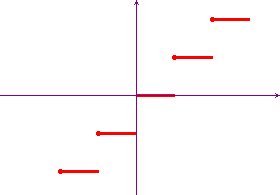
The function f(x) = [x] +
signum(x) in [-1,2]
![[x] times signum(x)](img/step.h11.gif)
-
The function f(x) = [x] ·
signum(x) in [-1,2].
![[x]+signum(x)](img/step.h12.gif)