The problem of areas
A preliminary example
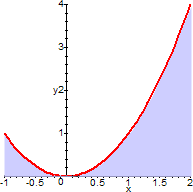
Consider the function f(x)=x2 and suppose you want to calculate the area bounded by the curve and the lines y=0, x=-1, x=2 (area between the function and the x-axis). Our knowledge of area, from Euclidean geometry, is restricted to simple geometric shapes such triangles, rectangles and other polygons, or to circles and their parts: the area in question cannot be calculated by a simple formula. One can try some approximation.
We consider the following two step functions:
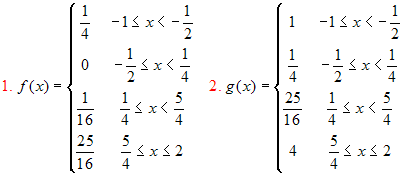
whose graphs are represented in green and pink here below.
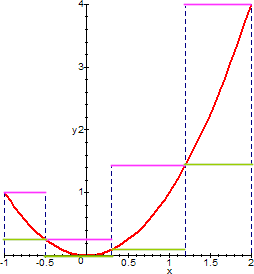
The areas between each function and the x-axis are, respectively, 21/4 and 87/64. Clearly these two numbers are far from the truth: the first is largely under-estimate, the second over-estimate. The approximations we have made are very crude indeed. But now we may ask: what does it happen if we consider other step functions closer to our function?
This is exactly what we want to investigate in this site: the answer to this question will lead us to the Riemann theory of integration.
What is area?
It's easy to define, in elementary geometry, the area of a rectangle: it is a number obtained multiplying the two sides of the figure. The definition can easily be extended to other plane figures, such as triangles and other polygons and, with much more care, to circles. Now we want to extend the concept of area to more complex shapes in the plane, so we need a precise definition of what area is.
The main fact is that area is a positive number that one can
assign to a class of plane figures that we shall call
measurable figures. This correspondence between figures
(that is subsets of the plane) and real numbers is what we
usually call a set function. As this function must
assign an area to figures, we'll call it a measure:
if M is the set of the subsets of the plane that we
want to measure, than a measure is a function 
. Obviously not all set functions can be measures. We
don't want to treat in detail this problem, but it's
obvious that such a function must have at least the following
properties:
- For all S in M, a(S) ≥ 0 (areas must not be negative!).
-
If S and T are in M, also their
union and intersection are in M and a(S
T) = a(S) + a(T) - a(S∩T).
- If S and T are in M, also their difference is in M and a(S \ T) = a(S) - a(S∩T).
- If S and T are in M, and T is congruent with S, than a(S) = a(T).
-
All rectangles are in M and if a rectangle R has sides p and q, than a(R) = pq (as a consequence, the area of a segment is always zero).
The Riemann theory of integration will lead us to the possibility of measuring a wide class of subsets of the real plane.