Properties of the integral of step functions
It's easy to prove the following geometric interpretation of the integral of a step function.
Given two numbers a and b and a step function
s whose domain is [a,b] (if a<b), or [b,a] (if
b<a),
consider the integral 
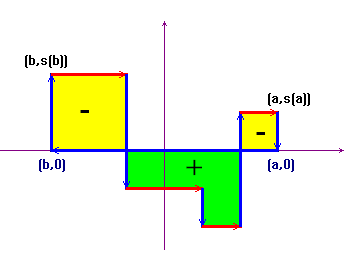
. Now draw the directed "path" from (a,0) to (b,0), to
(b,s(b)), to
(a,s(a)) and again to (a,0), as in the following picture. This path encloses some
regions, whose contour is sometimes clockwise and sometimes counterclockwise directed. We'll
consider as positive the areas whose contour is counterclockwise directed, as negative those whose
contour is clockwise directed. The integral is the algebraic sum of these areas.
Main properties
We now point out some fundamental properties of the integral of step functions. These properties are almost obvious if one keeps in mind the geometric interpretation and, for this reason, we leave the proof as an exercise. The most important fact is that all these properties remain unchanged also for the integral of more general functions, as we shall see.
- Linearity property. Given two step functions s and t and two real numbers
c and d, the following holds:
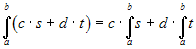
- Additive property with respect to the integration interval. Given three numbers
a, b and c (whose order is unimportant), and a step function
s, the
following holds:
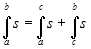. - Comparison property. Given two step functions s and t and two real numbers
a and b (with a < b), if s(x)≤t(x) for all
x in [a,b] then:
.
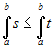