Introduzione alternativa al numero di Nepero
Esistono diverse strategie per introdurre il numero di Nepero, base dei logaritmi naturali e della funzione esponenziale più importante.
Qui vogliamo proporre un metodo a nostro avviso molto significativo, e facilmente trattabile anche senza ricorrere al concetto di limite.
Il problema che dà origine a questa trattazione è il seguente:
Dato un reale a>0, si considerino le funzioni
f(x)=xa (funzione potenza) e g(x)=ax (funzione esponenziale);
si esaminino le intersezioni tra i due grafici, per x>0, al variare di a.
È evidente che i due grafici si intersecano in corrispondenza di x=a, in quanto si ottiene, da entrambe le funzioni, aa. Il problema è di vedere se ci sono altre intersezioni e, in caso affermativo, quante.
La situazione è particolarmente semplice per a≤1, quando le due curve hanno il solo punto di intersezione x=a. La situazione per a=0.5 e per a=1 è rappresentata nei due grafici qui sotto. In questo caso una delle due funzioni è decrescente, mentre l'altra è crescente.
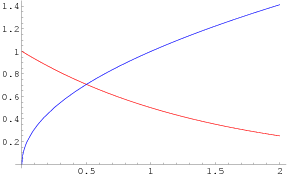
Nel caso a>1 la situazione diventa più interessante: le intersezioni sono sempre due, tranne nel caso in cui a=e, in cui le due curve sono tra di loro tangenti esattamente nel punto x=e, e non hanno altri punti comuni.
Le situazioni per 1<a<e, a=e e a>e rispettivamente sono rappresentate nei grafici qui sotto, dove è stato scelto a=2 nel primo e a=4 nel terzo.
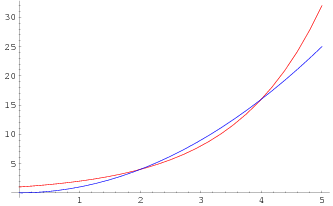
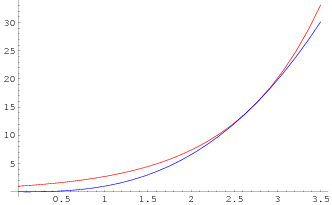
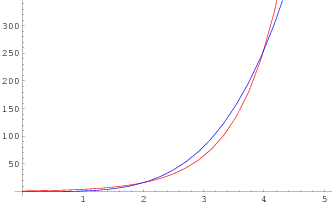
È interessante notare che, per 1<a<e, la prima intersezione si ha in corrispondenza di x=e, nel caso a>e è invece la seconda intersezione che si avviene in corrispondenza di x=e.
La verifica di quanto sopra, in particolare del fatto che per x=e le due curve sono tangenti, richiede il calcolo delle derivate, ma una verifica grafica con Cabri è abbastanza semplice, come si può vedere nell'animazione qui sotto, nella quale, variando a, puoi controllare che cosa succede, entro certi limiti.
In conclusione si può osservare che il numero di Nepero fa da separatore tra i due sottoinsiemi A e B dei reali maggiori di 1 così definiti:
- A è l'insieme degli a>1 per cui le due curve f(x)=xa e g(x)=ax si intersecano in due punti x1<x2, con x1=a;
- B è l'insieme degli a>1 per cui le due curve f(x)=xa e g(x)=ax si intersecano in due punti x1<x2, con x2=a.
Insomma questo numero di Nepero non finisce mai di sorprendere!