Calcolo del limite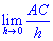 
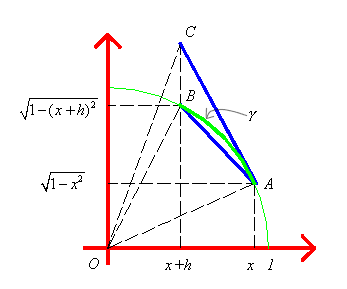
Per il calcolo di questo limite dobbiamo prima trovare
l'equazione della retta tangente alla circonferenza nel
punto A. Indicando con t la variabile nell'equazione della
retta (per non confonderla con x che, in questa fase, è
fissato), l'equazione si trova facilmente osservando che
e che le coordinate di A sono 
; si
trova:
.
Da qui si possono ricavare le coordinate di C:
.
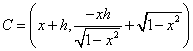Allora: 
e, tenendo conto che h<0,
.
Il calcolo del limite, per h tendente a zero, è ora
banale e porge: 
.