Dimostrazioni usando il calcolo differenziale
![]()
![]() . La funzione a primo membro è continua in
[-1,1] e derivabile all'interno con derivata ovunque nulla.
Il teorema sul limite della derivata assicura la
derivabilità anche agli esetrmi. Per il solito corollario
del teorema di Lagrange la funzione è allora costante e
basta calcolarne il valore in un punto per concludere sulla
validità della identità.
. La funzione a primo membro è continua in
[-1,1] e derivabile all'interno con derivata ovunque nulla.
Il teorema sul limite della derivata assicura la
derivabilità anche agli esetrmi. Per il solito corollario
del teorema di Lagrange la funzione è allora costante e
basta calcolarne il valore in un punto per concludere sulla
validità della identità.
![]()
![]() . La funzione a primo membro è continua in
R\{0}e derivabile con derivata ovunque nulla.
Non si può concludere che è costante, visto che il
dominio non è un intervallo. Essa è però
costante sui reali strettamente positivi e su quelli
strettamente negativi, che sono intervalli. Basterà
allora calcolare il valore in un punto per entrambi gli
intervalli per concludere sulla validità
dell'identità.
. La funzione a primo membro è continua in
R\{0}e derivabile con derivata ovunque nulla.
Non si può concludere che è costante, visto che il
dominio non è un intervallo. Essa è però
costante sui reali strettamente positivi e su quelli
strettamente negativi, che sono intervalli. Basterà
allora calcolare il valore in un punto per entrambi gli
intervalli per concludere sulla validità
dell'identità.
![]()
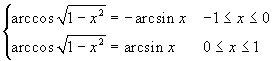 .Come nei due casi precedenti basta controllare
che la derivata del primo membro e quella del secondo membro
sono uguali e che in entrambi i casi si tratta di funzioni
definite su intervalli. Bisognerà inoltre verificare
l'uguaglianza su un punto.
.Come nei due casi precedenti basta controllare
che la derivata del primo membro e quella del secondo membro
sono uguali e che in entrambi i casi si tratta di funzioni
definite su intervalli. Bisognerà inoltre verificare
l'uguaglianza su un punto.
![]()
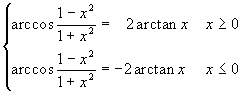 .Come nei due casi iniziali basta controllare che
la derivata del primo membro e quella del secondo membro sono
uguali e che in entrambi i casi si tratta di funzioni definite
su intervalli. Bisognerà inoltre verificare
l'uguaglianza su un punto.
.Come nei due casi iniziali basta controllare che
la derivata del primo membro e quella del secondo membro sono
uguali e che in entrambi i casi si tratta di funzioni definite
su intervalli. Bisognerà inoltre verificare
l'uguaglianza su un punto.
![]()
![]() . Come nei due casi iniziali basta controllare che
la derivata del primo membro e quella del secondo membro sono
uguali e che si tratta di funzioni definite su intervalli.
Bisognerà inoltre verificare l'uguaglianza su un
punto.
. Come nei due casi iniziali basta controllare che
la derivata del primo membro e quella del secondo membro sono
uguali e che si tratta di funzioni definite su intervalli.
Bisognerà inoltre verificare l'uguaglianza su un
punto.